�ő̔�M
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
1819�N�t�����X�̃f�������ƃv�e�B���A�퉷�ɂ����Čő̂���σ�����M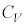 ���قƂ�ǂ̕�����
���قƂ�ǂ̕�����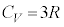 (
(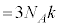
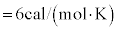 �CR�F�C�̒萔�A
�CR�F�C�̒萔�A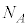 �F�A�{�K�h�����Ak�F�{���c�}���萔)�ł��邱��(�f�������E�v�e�B�̖@��)�����܂����B
�F�A�{�K�h�����Ak�F�{���c�}���萔)�ł��邱��(�f�������E�v�e�B�̖@��)�����܂����B
1971�N�I�[�X�g���A�̃{���c�}���́A�G�l���M�[�����z���Ɋ�Â��āA�f�������E�v�e�B�̖@����������܂����B�{���c�}���́A��������N�̌��q��N�̒��a�U���q�Ƃ��ĐU�����Ă���Ƃ��������u���܂����B1�̌��q��������m�C�p�U������ω�C�^������p�C�ʒu��q�Ƃ���ƁA�͊w�I�G�l���M�[(�n�~���g�j�A���ƌ����܂�)�́A
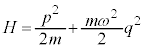 �@����@
�@����@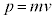 �C
�C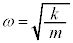 �Ȃ̂ŁA
�Ȃ̂ŁA
�ƂȂ��Ă��܂��B
�n���{���c�}�����z�ɏ]��(�ȉ�����Ή��x��T�Ƃ��āA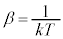 )�Ƃ��āA�ÓT�_�ɂ����Ă��^�����͘A���I�ɕω�����̂ŁA�^���G�l���M�[
)�Ƃ��āA�ÓT�_�ɂ����Ă��^�����͘A���I�ɕω�����̂ŁA�^���G�l���M�[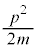 �̕��ϒl
�̕��ϒl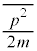 ��
��
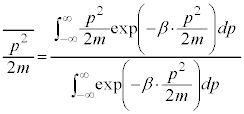 �@����A
�@����A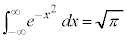 �@����B�@��p����ƁA
�@����B�@��p����ƁA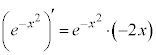 ���A
���A
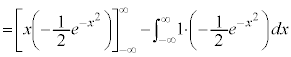
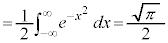 �@����C
�@����C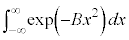 �́A�B�ŁA
�́A�B�ŁA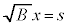 �Ƃ����ƁA
�Ƃ����ƁA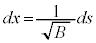 ���A
���A
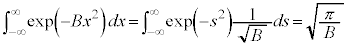 �@����D
�@����D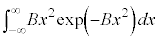 �́A�C�ŁA
�́A�C�ŁA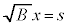 �Ƃ����ƁA
�Ƃ����ƁA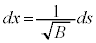 ���A
���A
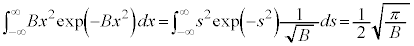 �@����E
�@����E
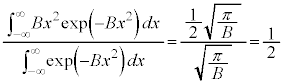 �@����F
�@����F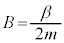 �Ƃ��āA
�Ƃ��āA
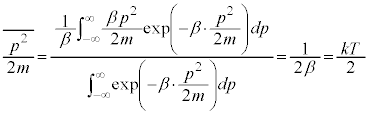 �@����G
�@����G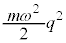 �̕��ϒl
�̕��ϒl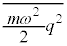 �́A�F�ŁA
�́A�F�ŁA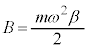 �Ƃ��āA
�Ƃ��āA
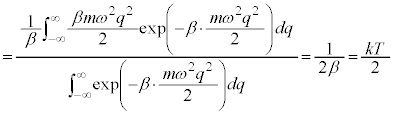 �@����H
�@����H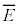 �́A
�́A
��������N�̌��q�̊e�X�ɂ��āAx�����Ay�����Az������3�̒��a�U���q������A�^���G�l���M�[���ʒu�G�l���M�[��6�̎��R�x������܂��BN�̌��q�S�̂�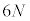 �̎��R�x������A���̊e�X��
�̎��R�x������A���̊e�X��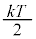 ���G�l���M�[���U�蕪������(�G�l���M�[�����z��)�̂ŁAn�����̌��q��������
���G�l���M�[���U�蕪������(�G�l���M�[�����z��)�̂ŁAn�����̌��q��������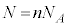 �Ƃ���ƁA�������S�G�l���M�[�́A
�Ƃ���ƁA�������S�G�l���M�[�́A
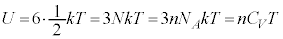 �@����I
�@����I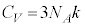 �ƂȂ�܂��B
�ƂȂ�܂��B
�Ƃ��낪�A�����Z�p�̌���ɂ��A�f�������E�v�e�B�̖@���́A�ቷ���A����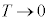 �Ƃ����
�Ƃ����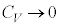 �ƂȂ�A�������炸��Ă��邱�Ƃ��킩���Ă��܂���(�_�C�A�����h�ȂǁA�퉷�ł���σ�����M��
�ƂȂ�A�������炸��Ă��邱�Ƃ��킩���Ă��܂���(�_�C�A�����h�ȂǁA�퉷�ł���σ�����M��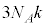 ��肩�Ȃ菬��������������)�B
��肩�Ȃ菬��������������)�B
1907�N�A�C���V���^�C���́A�f�������E�v�e�B�̖@�����ቷ�ł���Ă��錻�ۂ��A�v�����N�̗ʎq�������̂����Đ������܂����B�A�C���V���^�C���́A�ő̂̌��q�͑S�ēƗ��ɐU�����Ă�����̂Ƃ��āA�e�X���A�ʎq�����������悤�ɁA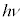 �C
�C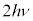 �C����Ƃ����ƂтƂт̒l���G�l���M�[�������A�{���c�}�����z�ɏ]�����̂Ƃ��čl�@���s���܂����B����ɂ��ƁA�e�U���q���G�l���M�[
�C����Ƃ����ƂтƂт̒l���G�l���M�[�������A�{���c�}�����z�ɏ]�����̂Ƃ��čl�@���s���܂����B����ɂ��ƁA�e�U���q���G�l���M�[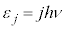 (
(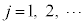 )�����m��
)�����m��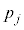 �́A
�́A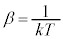 �Ƃ��āA
�Ƃ��āA
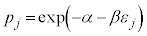 �@(�ȉ��A�w����
�@(�ȉ��A�w����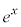 ��
��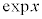 �Ə����܂�)
�Ə����܂�)
�G�l���M�[�̊��Ғl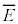 �́A
�́A
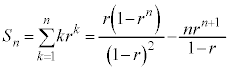 ���An���[���ɑ傫���A
���An���[���ɑ傫���A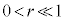 �̂Ƃ��ɂ́A
�̂Ƃ��ɂ́A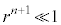 �C
�C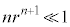 ���A
���A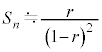 �C������g����
�C������g����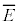 �́A
�́A
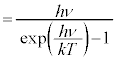 �@����J
�@����J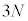 �����āA�S�G�l���M�[U�́A
�����āA�S�G�l���M�[U�́A
��σ�����M�́AU��T�ɔ�Ⴕ�Ȃ��̂ŁA�����ł͇I�Ƃ͈���āA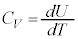 �Ƃ��Čv�Z���܂��B
�Ƃ��Čv�Z���܂��B
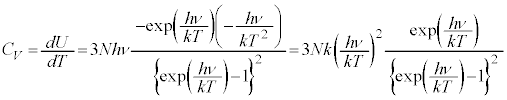 �@����K
�@����K
�K�́A������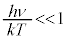 �̂Ƃ��ɂ́A
�̂Ƃ��ɂ́A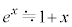 (
(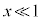 )�C
)�C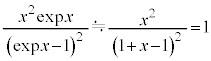 ���A
���A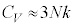 �ƂȂ�f�������E�v�e�B�̖@���Ɉ�v���܂��B
�ƂȂ�f�������E�v�e�B�̖@���Ɉ�v���܂��B
�ቷ��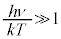 �̂Ƃ��ɂ́A�K�����1�������ł��āA�w�����I��0�ɋ߂Â��܂��B���肱�ݗ��_�Ńm�[�x���܂���܂������i�U��Y���m�́A������A�[��������
�̂Ƃ��ɂ́A�K�����1�������ł��āA�w�����I��0�ɋ߂Â��܂��B���肱�ݗ��_�Ńm�[�x���܂���܂������i�U��Y���m�́A������A�[��������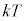 �Ƃ����[���ɑ傫���e����G�l���M�[�ʎq
�Ƃ����[���ɑ傫���e����G�l���M�[�ʎq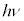 �͗e��̑̐ς����܂œ���̂Ŕ�M��
�͗e��̑̐ς����܂œ���̂Ŕ�M��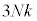 �ɂȂ邪�A�ቷ�ɂȂ���
�ɂȂ邪�A�ቷ�ɂȂ���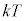 �Ƃ��������ȗe��ɂȂ�ƁA�G�l���M�[�ʎq
�Ƃ��������ȗe��ɂȂ�ƁA�G�l���M�[�ʎq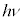 ���e��̑̐ϕ��܂œ���Ȃ��Ȃ�(�����ȃR�b�v�Ɋp����������C���[�W)�̂Ŕ�M���������Ȃ�A�Ƃ����悤�ɗʎq�����Ɋ�Â��Đ������܂����B
���e��̑̐ϕ��܂œ���Ȃ��Ȃ�(�����ȃR�b�v�Ɋp����������C���[�W)�̂Ŕ�M���������Ȃ�A�Ƃ����悤�ɗʎq�����Ɋ�Â��Đ������܂����B
���D��L�ł́A��_�G�l���M�[�������čl���Ă��܂��B���ۂɂ́A�s�m�萫�����ɂ��A�G�l���M�[���[���̏�Ԃ͋����ꂸ�A��Η�x�ɂ����Ă����a�U���q���G�l���M�[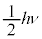 �������Ƃ��킩���Ă��܂��B
�������Ƃ��킩���Ă��܂��B
���̌�A�A�C���V���^�C���̗��_�ł́A�ቷ��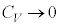 �ƂȂ�̂������l�����}�������邱�Ƃ����炩�ɂȂ�A1912�N�I�����_�̃f�o�C�ɂ����ǂ���A�����l�ɋ߂����_����o����܂����B
�ƂȂ�̂������l�����}�������邱�Ƃ����炩�ɂȂ�A1912�N�I�����_�̃f�o�C�ɂ����ǂ���A�����l�ɋ߂����_����o����܂����B
�f�o�C�́A1��L�̒e���̒��̌��q�̐U�������g�̂悤�ɍl���A����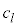 �̏c�g������
�̏c�g������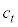 �̉��g�ɕ����čl���܂����B�v�����N�������t���̗��_�Ɠ��l�ɁAx�����Ay�����Az�������U��������{�U������
�̉��g�ɕ����čl���܂����B�v�����N�������t���̗��_�Ɠ��l�ɁAx�����Ay�����Az�������U��������{�U������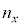 �C
�C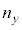 �C
�C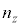 �{(
�{(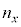 �C
�C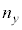 �C
�C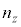 �F���R���A
�F���R���A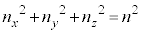 )�Ƃ��āA
)�Ƃ��āA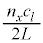 �C
�C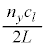 �C
�C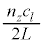 �̂悤�ɕ\���A�c�g���U����
�̂悤�ɕ\���A�c�g���U����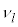 �ɂ��āA
�ɂ��āA
���a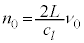 �̋����ɑ��݂���i�q�_
�̋����ɑ��݂���i�q�_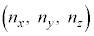 �̐��́A���̑̐ς�
�̐��́A���̑̐ς�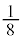 �Ƃ��āA
�Ƃ��āA
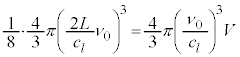 �@(
�@(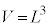 �͒e���̂̑̐�)
�͒e���̂̑̐�)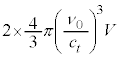
�U������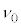 ��菬������Ԑ��́A
��菬������Ԑ��́A
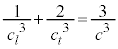 �Ƃ��āA
�Ƃ��āA
�f�o�C�́A�����ŁA��Ԑ���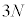 �ł����āA�U����
�ł����āA�U����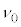 �ɏ��
�ɏ��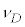 ������ƍl���܂����B
������ƍl���܂����B
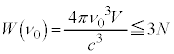 �@��
�@�� 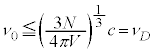 �@����L
�@����L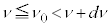 �͈̔͂ɂ����Ԑ���
�͈̔͂ɂ����Ԑ���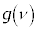 �Ƃ���ƁA
�Ƃ���ƁA
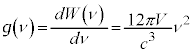 �@(
�@(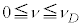 )
)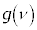 �ƇJ��
�ƇJ��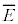 �̐ςƂ��āA�U����ν�ɑ����G�l���M�[�́A
�̐ςƂ��āA�U����ν�ɑ����G�l���M�[�́A
�S�G�l���M�[U�́A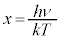 �Ƃ������u���ϕ�����ƁA
�Ƃ������u���ϕ�����ƁA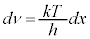 �Cν�F
�Cν�F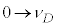 �̂Ƃ��Ax�F
�̂Ƃ��Ax�F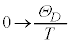 (
(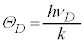 �F�f�o�C���x�ƌ����܂��@����M)���A
�F�f�o�C���x�ƌ����܂��@����M)���A
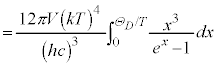 �@����N
�@����N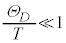 ���A��ϕ�����
���A��ϕ�����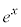 ��
��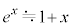 �Ƃ݂ćN�́A
�Ƃ݂ćN�́A
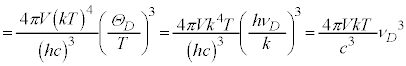 �@(�L�C�M����)
�@(�L�C�M����)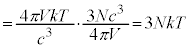
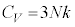 �ł���A����̓f�������E�v�e�B�̖@���ł��B
�ł���A����̓f�������E�v�e�B�̖@���ł��B
�ቷ�ŁA�N�ɂ�����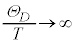 �ƌ��Ȃ���Ƃ��́A
�ƌ��Ȃ���Ƃ��́A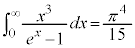 �@(�v�Z�͏ȗ�)���A
�@(�v�Z�͏ȗ�)���A
������σ�����M�͎����l�Ƃ悭��v���܂��B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@������b����TOP�@�@����TOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 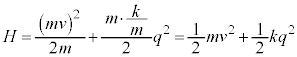
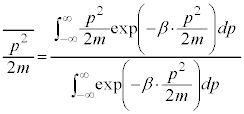 �@����A
�@����A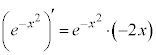 ���A
���A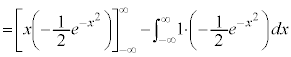
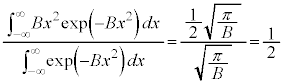 �@����F
�@����F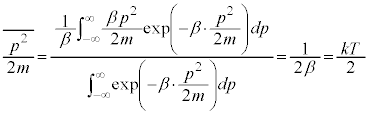 �@����G
�@����G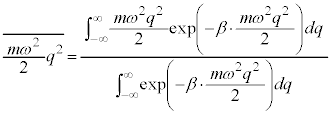
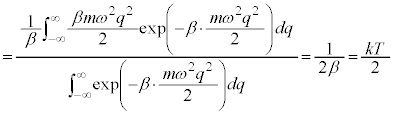 �@����H
�@����H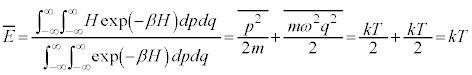
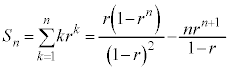 ���An���[���ɑ傫���A
���An���[���ɑ傫���A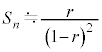 �C������g����
�C������g����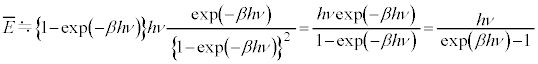
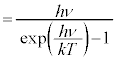 �@����J
�@����J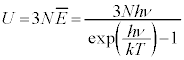
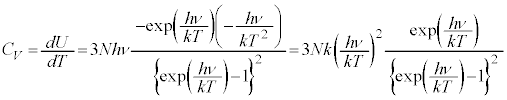 �@����K
�@����K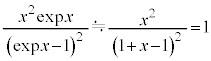 ���A
���A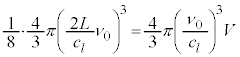 �@(
�@(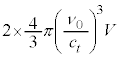
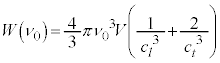
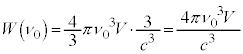
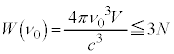 �@��
�@�� 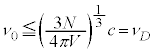 �@����L
�@����L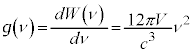 �@(
�@(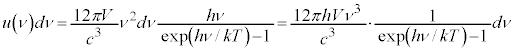
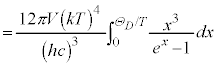 �@����N
�@����N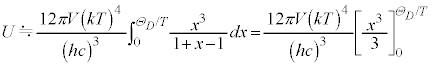
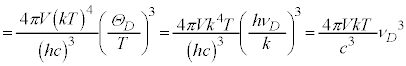 �@(�L�C�M����)
�@(�L�C�M����)