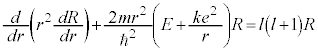�ʎq�͊w�̊�b(����2)����̂Â��ł��B
�V�����[�f�B���K�[���������g���Đ��f���q�ׂĂ݂܂��傤�B�ڍׂȌv�Z�͑�ςȂ̂Ŋ������܂����A��w�i�w��Ɋm���߂Ă��������B
���f���q�ł́A�d�q�����q�j�̉�������悤�ȃ��f����z�肷��̂ŁA�{�[�A�̌��q�͌^�Ɠ��l�ɁA�p�^����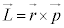 ���l���܂�(�ʐϑ��x���Q��)�B
���l���܂�(�ʐϑ��x���Q��)�B
���f���q�̏ꍇ�A�ʒu�G�l���M�[�́A�N�[�����͂̈ʒu�G�l���M�[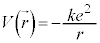 (k�F�N�[�����͂̔��萔�Ce�F�d�C�f��)�ł��B�d�q���]���V�����[�f�B���K�[�������́A
(k�F�N�[�����͂̔��萔�Ce�F�d�C�f��)�ł��B�d�q���]���V�����[�f�B���K�[�������́A
���f���q�ł͋��Ώ̂ȏ������̂ŁA�����W�n�ōl���܂��B�����W�n�ł́A���v���X���Z�qΔ�́A
�ɂȂ�(�������W�n�E�~�����W�n�E�����W�n���Q��)�̂ŁA�V�����[�f�B���K�[�������͋����W�n�ł́A
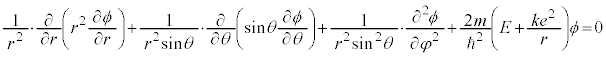
�ƂȂ�܂��B�ϐ���������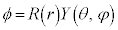 �Ƃ����đ������ƁA
�Ƃ����đ������ƁA
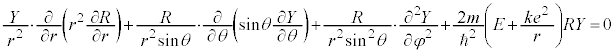
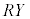 �Ŋ���
�Ŋ���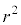 ��������ƁA
��������ƁA
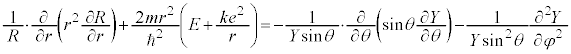
���ӂ�r�݂̂̊��A�E�ӂ�θ�Cφ�݂̂̊��Ȃ̂ŁA���̒l�͒萔�ŁA�����L�Ƃ����ƁA
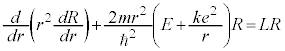 �@����A
�@����A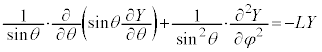 �@����B
�@����B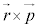 ���l���܂�(�ʐϑ��x���Q��)�B
���l���܂�(�ʐϑ��x���Q��)�B
�ʎq���̌���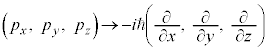 ��K�p���A�����W�ւ̕ϊ����s���ƁA
��K�p���A�����W�ւ̕ϊ����s���ƁA
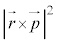 ��
��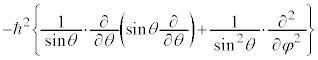
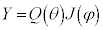 �Ƃ����ćB�ɑ������ƁA
�Ƃ����ćB�ɑ������ƁA
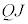 �Ŋ���
�Ŋ���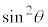 ��������ƁA
��������ƁA
���ӂ�θ�݂̂̊��A�E�ӂ�φ�݂̂̊��Ȃ̂ŁA���̒l�͒萔�ŁA�����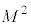 �Ƃ����ƁA
�Ƃ����ƁA
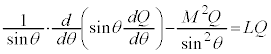 �@����C
�@����C
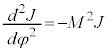 �@����D
�@����D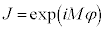 �ƂȂ�܂����A
�ƂȂ�܂����A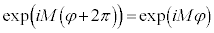 ���A
���A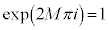 ���K�v��M�͐����Ɍ����܂��B
���K�v��M�͐����Ɍ����܂��B
�C�́A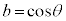 �Ƃ����ƁA
�Ƃ����ƁA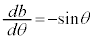 ���A
���A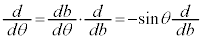 ���A
���A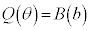 �Ƃ��āA
�Ƃ��āA
���̉��́A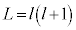 (
(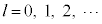 )�̂Ƃ��A���W�����h���̔�������
)�̂Ƃ��A���W�����h���̔�������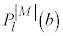 (
(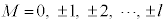 )�ƌĂ����ɂȂ邱�Ƃ��킩���Ă��܂��B
)�ƌĂ����ɂȂ邱�Ƃ��킩���Ă��܂��B
�ȂǂƂȂ��Ă��܂��B
�B�̉��F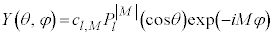 (
(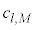 �͑S�m����1�ƂȂ�悤�Ɍ��܂�萔)�����ʒ��a���ƌ����܂��B
�͑S�m����1�ƂȂ�悤�Ɍ��܂�萔)�����ʒ��a���ƌ����܂��B
���āA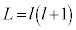 �Ƃ��āA�A�́A
�Ƃ��āA�A�́A
���̉��́A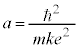 �C
�C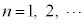 �C�Ƃ��āA
�C�Ƃ��āA
 �C
�C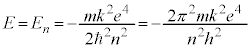
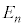 �̒l���{�[�A�̌��q�͌^�ɂ�����l�ƈ�v���܂��B�����ŁA
�̒l���{�[�A�̌��q�͌^�ɂ�����l�ƈ�v���܂��B�����ŁA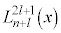 �̓��Q�[���̔��������ƌĂ�鑽�����ŁA
�̓��Q�[���̔��������ƌĂ�鑽�����ŁA
�ȂǂƂȂ��Ă��܂��B
���f���q�̓d�q���]���g�����́A���ʒ��a���ƃ��Q�[���̔������������������̂ɂȂ�܂��B
���Q�[���̔��������ł́A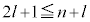 �C�܂�A
�C�܂�A �Ƃ����������t���܂��B
�Ƃ����������t���܂��B
���W�����h���̔��������ł́Al�ɑ��āA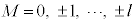 �Ƃ����W(
�Ƃ����W(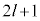 �ʂ��M�̒l���\�ŁA
�ʂ��M�̒l���\�ŁA �d�ɏk�ނ��Ă���A�ƌ����܂�)������܂��B
�d�ɏk�ނ��Ă���A�ƌ����܂�)������܂��B
���f���q(�d�q��1�̑��̌��q�����l�ł�)�ł́A�d�q�ɂ��āA
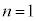 �̂Ƃ�
�̂Ƃ�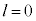 (1s�O��)�̂݉\�ŁA���̂Ƃ�
(1s�O��)�̂݉\�ŁA���̂Ƃ�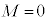 �̂݁B
�̂݁B
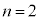 �̂Ƃ�
�̂Ƃ�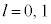 ���\�ŁA
���\�ŁA
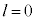 (2s�O��)�Ȃ�
(2s�O��)�Ȃ�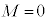 �̂݁A
�̂݁A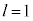 (2p�O��)�Ȃ�
(2p�O��)�Ȃ�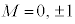
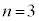 �̂Ƃ�
�̂Ƃ�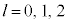 ���\�ŁA
���\�ŁA
 (3s�O��)�Ȃ�
(3s�O��)�Ȃ�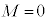 �̂݁A
�̂݁A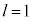 (3p�O��)�Ȃ�
(3p�O��)�Ȃ�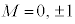 �C
�C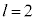 (3d�O��)�Ȃ�
(3d�O��)�Ȃ�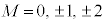
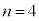 �̂Ƃ�
�̂Ƃ�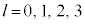 ���\�ŁA
���\�ŁA
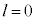 (4s�O��)�Ȃ�
(4s�O��)�Ȃ�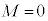 �̂݁A
�̂݁A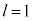 (4p�O��)�Ȃ�
(4p�O��)�Ȃ�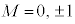 �C
�C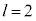 (4d�O��)�Ȃ�
(4d�O��)�Ȃ�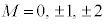 �C
�C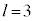 (4f�O��)�Ȃ�
(4f�O��)�Ȃ�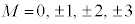
n����ʎq���Al����ʗʎq���AM�����C�ʎq��(��L�ł�m��d�q�̎��ʂƂ��Ă��܂����A��发�ł́A���C�ʎq����m�ŕ\�����Ƃ����ʂł�)�ƌ����܂��B�d�q�̏�Ԃ́A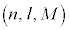 �̑g�Ō��܂�܂����A1922�N�Ƀh�C�c�̃V���e�����ƃQ�����b�n���s���������ɂ��ƁA����̊p�^���ʂ������Ă���͂��̋◱�q�����ꒆ��ʉ߂�����ƃr�[����2�ɕ������̂ł��B���̌��ʂ́A�����
�̑g�Ō��܂�܂����A1922�N�Ƀh�C�c�̃V���e�����ƃQ�����b�n���s���������ɂ��ƁA����̊p�^���ʂ������Ă���͂��̋◱�q�����ꒆ��ʉ߂�����ƃr�[����2�ɕ������̂ł��B���̌��ʂ́A�����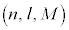 �ł����Ă��A2�̏�Ԃɕ������A�Ƃ������Ƃ��Ӗ����Ă��܂����B
�ł����Ă��A2�̏�Ԃɕ������A�Ƃ������Ƃ��Ӗ����Ă��܂����B
��ɁA�d�q�ɃX�s���Ƃ�������������A������̃X�s���A�������̃X�s����2�̏�Ԃ������Ă��āA���ꒆ��ʉ߂�����ƁA�X�s���̈Ⴂ�ɂ���ăr�[����2�ɕ�����邱�Ƃ�������܂����B�܂�A1�g��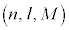 ��2�̏�Ԃ����̂ł��B�܂��A��ʎq���A���ʗʎq���A���C�ʎq���A�X�s���ɂ���ēd�q�̏�Ԃ�1�ɒ�܂�A���A1�̌��q�ŕ����̓d�q������̏�ԂɂȂ邱�Ƃ͂Ȃ��A1�̏�Ԃ̓d�q��1�����Ȃ�(�p�E���̔r�����ƌ����܂�)���Ƃ��킩��܂����B
��2�̏�Ԃ����̂ł��B�܂��A��ʎq���A���ʗʎq���A���C�ʎq���A�X�s���ɂ���ēd�q�̏�Ԃ�1�ɒ�܂�A���A1�̌��q�ŕ����̓d�q������̏�ԂɂȂ邱�Ƃ͂Ȃ��A1�̏�Ԃ̓d�q��1�����Ȃ�(�p�E���̔r�����ƌ����܂�)���Ƃ��킩��܂����B
���f���q�̏ꍇ�A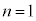 ��K�k�A
��K�k�A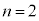 ��L�k�A
��L�k�A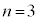 ��M�k�A
��M�k�A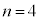 ��N�k�A�Ƃ����悤�ɁA��ʎq���ɂ���ĈقȂ锼�a�̋O���������Ă��܂��B
��N�k�A�Ƃ����悤�ɁA��ʎq���ɂ���ĈقȂ锼�a�̋O���������Ă��܂��B
K�k�ɂ�1s�O����2�̓d�q������܂��BL�k�ɂ�2s�O����2�C2p�O����3�ʂ�̏�Ԃ�6�̓d�q������v8�̓d�q������܂��BM�k�ł́A3s�O����2�A3p�O����3�ʂ�̏�Ԃ�6�A3d�O��5�ʂ�̏�Ԃ�10�A�v18�̓d�q������܂��B���l�ɍl���āAN�k�ɂ́A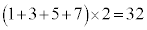 �̓d�q������܂��B
�̓d�q������܂��B
���f���q�ȊO�ł����l�̓d�q�̓����������Ƃ��āA���q�j�͓d�q�Ɠ������̗z�q(���d��)�������Ă��āA�z�q�̐������q�ԍ��ɂȂ��Ă��܂��B�e���q�́A�G�l���M�[�̒Ⴂ���Ɏ�ʎq���̏������O�����珇�ɓd�q�������čs���܂��B
K�k�ł́A
1s�O���ɁA�d�q��1���鐅�fH(���q�ԍ�1)��2����w���E��He(���q�ԍ�2)�C
�����L�k�ł́A
2s�O���ɁA�d�q��1���郊�`�E��Li(���q�ԍ�3)��2����x�����E��Be(���q�ԍ�4)�C
����ɁA2p�O���ɓd�q��1�`6����A�z�E�fB(���q�ԍ�5)�C�Y�fC(���q�ԍ�6)�C���fN(���q�ԍ�7)�C�_�fO(���q�ԍ�8)�C�t�b�fF(���q�ԍ�9)�C�l�I��Ne(���q�ԍ�10)�C
����ɁAM�k�ł́A
3s�O���ɓd�q��1����i�g���E��Na(���q�ԍ�11)�C2����}�O�l�V�E��Mg(���q�ԍ�12)�C
����ɁA3p�O���ɓd�q��1�`6����AAl(13)�CSi(14)�CP(15)�CS(16)�CCl(17)�CAr(18)�C
���̌�́A3d�O���ɓd�q�����錴�q�ł͂Ȃ��A3d�O�����G�l���M�[���Ⴂ4s�O���̕��ɓd�q���l�܂��Ă����܂��B
N�k�ł́A
4s�O���ɓd�q��1����K(19)�C2����Ca(20)�Ƒ����A��������͕��G�ȓ���������܂����A
4s�O���ɓd�q��2����A����ɁA3d�O���ɓd�q��1����Sc(21)�C2����Ti(22)�C3����V(23)�C
���̎��́A4s�O���̓d�q��1��3d�O���ɓd�q��5����Cr(24)�������A
�Ă�4d�O���ɓd�q��2�A3d�O���ɓd�q��5��Mn(25)�C6��Fe(26)�C7��Co(27)�C8��Ni(28)�C
4s�O���̓d�q��1�A3d�O���̓d�q��10��Cu(29)�C�����M�k�͖����ɂȂ�܂��B
���́A
4s�O����2��Zn(30)�A
����ɁA4p�O����1�`6����Ga(31)�CGe(32)�CAs(33)�CSe(34)�CBr(35)�CKr(36)�Ƒ�������́A
����ɁA5s�O���ɓd�q��1����Rb(37)�C2����Sr(38)�C
����ɁA4d�O����1����Y(39)�C2����Zr(40)�Ƃ�����ɕs�K���ȓ����������悤�ɂȂ�܂��B�K��������ʎq���̑傫�������傫�ȃG�l���M�[�ɂȂ�Ƃ͌���Ȃ����߂ł��B
�ȏ�ɂ��A�e�k�������ɂȂ�AHe�CNe�C3p�O���A4p�O���܂ŋl�܂�Ar�CKr������Ȍ��q�ł��邱�ƁA�O�k�ɓd�q��1������Li�CNa�CK���O�k�d�q����o���₷�����������������ƁA���l��1�s�����Ă����F�CCl�CBr�CI�̂悤�ȃn���Q�����������������Ȃ邱�ƂȂǁA���f���q���̓d�q�̋������𖾂��ꂽ���Ƃɂ��A�������\�������ł��܂����B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@������b����TOP�@�@����TOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 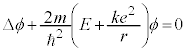
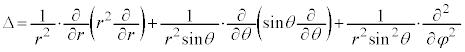
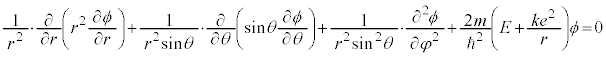
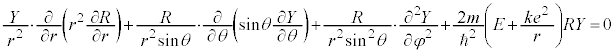
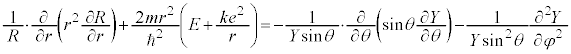
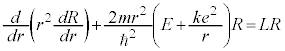 �@����A
�@����A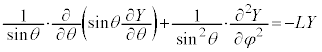 �@����B
�@����B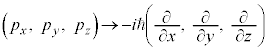 ��K�p���A�����W�ւ̕ϊ����s���ƁA
��K�p���A�����W�ւ̕ϊ����s���ƁA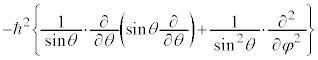
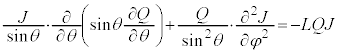

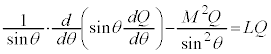 �@����C
�@����C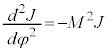 �@����D
�@����D