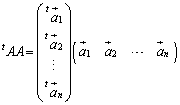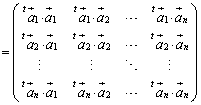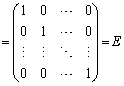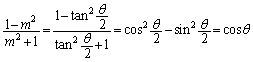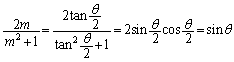1���ϊ�(����2)�@�@�@�֘A���
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
1���ϊ��̂Â��ł��B
1���ϊ�f�Cg�̕\���s���A�CB�Ƃ���B�x�N�g��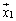 �ɑ��āA
�ɑ��āA
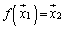 �C
�C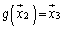 �̂Ƃ��A
�̂Ƃ��A
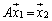 �C
�C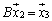
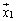 ����
����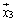 �ւ̑Ή���f�Cg�������ϊ��ƌ����A
�ւ̑Ή���f�Cg�������ϊ��ƌ����A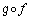 �ƕ\���B
�ƕ\���B
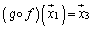 �ł���A
�ł���A
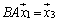
�ƂȂ�̂ŁA�����ϊ�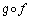 �̕\���s���
�̕\���s���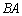
�܂��A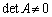 �ł����āA
�ł����āA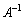 �����݂���Ƃ��A
�����݂���Ƃ��A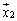 ����
����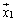 �ւ̑Ή���f���t�ϊ��ƌ����A
�ւ̑Ή���f���t�ϊ��ƌ����A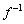 �ƕ\���B
�ƕ\���B
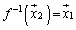 �ł���A
�ł���A
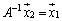
�ƂȂ�̂ŁA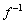 �̕\���s���
�̕\���s���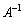
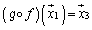 �Ə����Ƃ��A�܂��A
�Ə����Ƃ��A�܂��A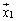 ��f����p���A����g����p���܂��B
��f����p���A����g����p���܂��B
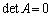 �̏ꍇ�ɂ́A�C�ӂ̃x�N�g��
�̏ꍇ�ɂ́A�C�ӂ̃x�N�g��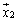 ���Ƃ��āA
���Ƃ��āA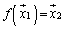 ����
����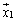 �����߂���킯�ł͂���܂���B���̂Ƃ��ɂ�f�̋t�ϊ��͑��݂��܂���B
�����߂���킯�ł͂���܂���B���̂Ƃ��ɂ�f�̋t�ϊ��͑��݂��܂���B
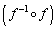 �C
�C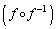 �́A
�́A ���A�P���ϊ��ł��B
���A�P���ϊ��ł��B
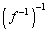 �́A
�́A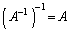 ���A���Ƃ̕ϊ�f�ł��B
���A���Ƃ̕ϊ�f�ł��B
1���������Ă����܂��B(�s���A�s��̐����Q��)
n�������s��A��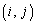 ������
������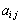 �Ƃ��āAA�̓]�u�s��
�Ƃ��āAA�̓]�u�s��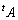 ��
��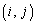 ������
������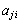 �ł��B
�ł��B
n�������s��B��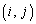 ������
������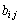 �Ƃ��āA
�Ƃ��āA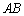 ��
��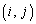 �����́A
�����́A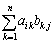 �ł��B
�ł��B
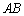 �̓]�u�s��
�̓]�u�s��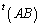 ��
��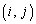 �����́A
�����́A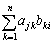 �ł��B������A
�ł��B������A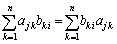 �ƌ���ƁA
�ƌ���ƁA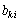 ��
��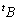 ��
��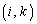 �����A
�����A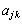 ��
��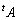 ��
��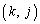 �����Ȃ̂ŁA
�����Ȃ̂ŁA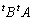 ��
��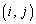 �����ƌ��邱�Ƃ��ł��܂��B
�����ƌ��邱�Ƃ��ł��܂��B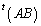 ��
��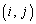 ������
������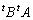 ��
��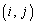 �����ɓ������̂ŁA
�����ɓ������̂ŁA
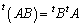
�����藧���܂��B
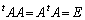 ����n�������s��A���s��ƌ����B�܂��A�����s��̕\��1���ϊ���ϊ��ƌ����B�����s��A�ɂ��āA
����n�������s��A���s��ƌ����B�܂��A�����s��̕\��1���ϊ���ϊ��ƌ����B�����s��A�ɂ��āA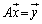 �ł���Ƃ��A
�ł���Ƃ��A
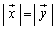
�����藧�B�܂�A����ϊ��́A�x�N�g���̑傫����ς��Ȃ��ϊ��ł���B
2�������s��A�������s��ł���Ƃ��AA�̕\��1���ϊ��́A
(i) 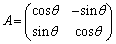 ���\���A�pθ �̉�]�ړ�
���\���A�pθ �̉�]�ړ�
(ii) 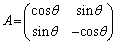 ���\���A�����F
���\���A�����F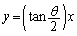 �Ɋւ���Ώ̈ړ�
�Ɋւ���Ώ̈ړ�
�̂ǂ��炩�Ɍ�����B
���wB�ň���������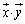 �́A�s��̐�
�́A�s��̐�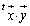 �ɑ������܂��B
�ɑ������܂��B
n������ԓ��̃x�N�g��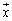 �C
�C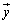 �̓��ρF
�̓��ρF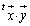 ��1���ϊ��ɍۂ��ĕۑ������A�x�N�g���̑傫���͕ς��܂���B
��1���ϊ��ɍۂ��ĕۑ������A�x�N�g���̑傫���͕ς��܂���B
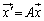 �C
�C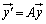 �Ƃ��āA
�Ƃ��āA
���ς��s��A�̕\��1���ϊ��ɂ����ĕۑ������̂ł���A
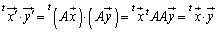
�����Ȃ邽�߂ɂ́A
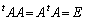
�ł���悢���ƂɂȂ�܂��B���̐��������s�����s��ł��B
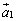 �C
�C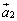 �C����C
�C����C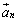 ���x�N�g�����Ƃ��āA
���x�N�g�����Ƃ��āA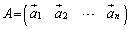 �Ə������Ƃ��܂��B
�Ə������Ƃ��܂��B
�����s��̏����́A
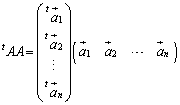
�@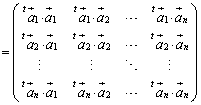
�@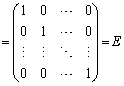
���ꂪ��������邽�߂ɂ́A�N���l�b�J�[��δ�L��(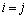 �̂Ƃ�
�̂Ƃ�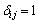 �C
�C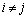 �̂Ƃ�
�̂Ƃ�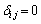 )��p���āA
)��p���āA
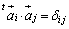
�܂�A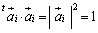 �@����@
�@����@
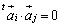 (
(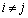 )�@����A
)�@����A
�@���A��x�N�g��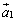 �C
�C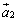 �C����C
�C����C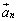 �͂�������P�ʃx�N�g���ł��B
�͂�������P�ʃx�N�g���ł��B
�A���A��x�N�g���݂͌��ɒ������܂��B
�܂�A�����s��͐��K�������ƂȂ�x�N�g�������ɕ��ׂĂł��Ă���s��ł�(���x�N�g�����c�ɕ��ׂ��A�ƁA���邱�Ƃ��ł���)�B
2�������s��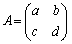 �Œ����s��ƂȂ���̂��l���Ă݂܂��B��L�ɂ��A��x�N�g��(���x�N�g��)�͒P�ʍs��ł����āA�݂��ɓ��ς�0�ƂȂ�̂ŁA
�Œ����s��ƂȂ���̂��l���Ă݂܂��B��L�ɂ��A��x�N�g��(���x�N�g��)�͒P�ʍs��ł����āA�݂��ɓ��ς�0�ƂȂ�̂ŁA
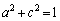 �@����B
�@����B
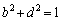 �@����C
�@����C
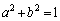 �@����D
�@����D
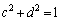 �@����E
�@����E
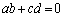 �@����F
�@����F
�B���A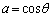 �C
�C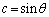 �Ƃ����܂��B
�Ƃ����܂��B
�D���A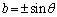
�E���A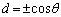
�F���A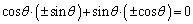
���̂��������ňӖ��̂���g�ݍ��킹�́A
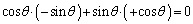 �C�܂�A
�C�܂�A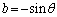 �C
�C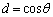
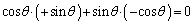 �C�܂�A
�C�܂�A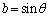 �C
�C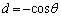
�]���āA2�������s��Œ����s��ƂȂ���̂́A�ȉ���2�ʂ�Ɍ����܂��B
(i) 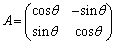
(ii) 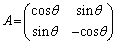
(i)�́A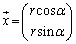 �Ƃ����x�N�g���ɂ�����ƁA
�Ƃ����x�N�g���ɂ�����ƁA
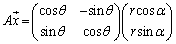
�@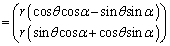
�@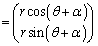
����āA�s��A�̕\��1���ϊ��́A���_�̂܂��Ƀx�N�g��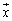 ���pθ ������]�ړ������邱�Ƃ��Ӗ����Ă��܂��B
���pθ ������]�ړ������邱�Ƃ��Ӗ����Ă��܂��B
(ii)�́A�����F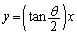 �@����G�@�Ɋւ���Ώ̈ړ�(���W���ʂɂ�����Ώ����Q��)��\���Ă���̂ł����A
�@����G�@�Ɋւ���Ώ̈ړ�(���W���ʂɂ�����Ώ����Q��)��\���Ă���̂ł����A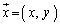 ��
��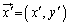 ���G�Ɋւ��đΏ̂��Ƃ���ƁA
���G�Ɋւ��đΏ̂��Ƃ���ƁA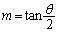 �Ƃ��āA
�Ƃ��āA
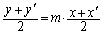 �C
�C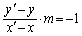
�� 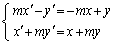
�s���p���ĕ\���ƁA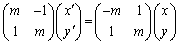
���ӂɍ�����A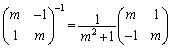 ��������ƁA
��������ƁA
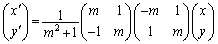
�@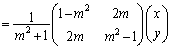
2�{�p�̌������A
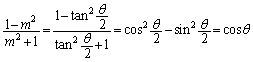
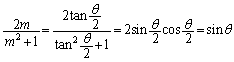
����āA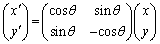
����Ŋm���߂��܂����B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���w��b����TOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B