���W���ʂɂ�����Ώ��@�@�@�֘A���
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�_�Ɋւ��đΏ̂Ȑ}�`
�_A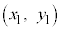 �Ɠ_B
�Ɠ_B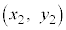 ���A�_P
���A�_P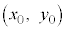 �Ɋւ��đΏ̂ł���Ƃ��A
�Ɋւ��đΏ̂ł���Ƃ��A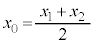 �C
�C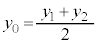
�_P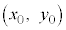 �Ɋւ��āA�������F
�Ɋւ��āA�������F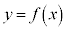 �ŕ\�����}�`�ƑΏ̂Ȑ}�`�́A
�ŕ\�����}�`�ƑΏ̂Ȑ}�`�́A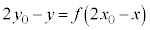
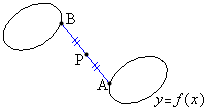 �E�}�̂悤�ɁA�_A
�E�}�̂悤�ɁA�_A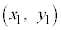 �Ɠ_B
�Ɠ_B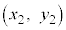 ���A�_P
���A�_P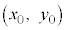 �Ɋւ��đΏ̂ł���Ƃ��A�_P�͐���AB�����_�ł��B
�Ɋւ��đΏ̂ł���Ƃ��A�_P�͐���AB�����_�ł��B
�� 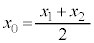 �C
�C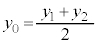 ����@
����@
�܂��A�_A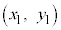 ���������F
���������F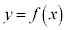 �ŕ\�����}�`��̓_�ł���Ƃ��A
�ŕ\�����}�`��̓_�ł���Ƃ��A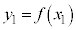 �����藧���܂��B���̂Ƃ��A�_P�Ɋւ��ē_A�ƑΏ̂ȓ_B
�����藧���܂��B���̂Ƃ��A�_P�Ɋւ��ē_A�ƑΏ̂ȓ_B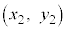 �����������������l���Ă݂܂��B
�����������������l���Ă݂܂��B
�@���A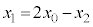 �C
�C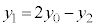 �����藧�̂ŁA������A
�����藧�̂ŁA������A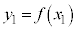 �ɑ������ƁA
�ɑ������ƁA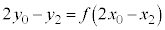 ����A
����A
�A���A�_B�̖������������ł��B�_A���A�}�`�F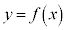 ��̓_���Ƃ���A�_B�́A�_P�Ɋւ��Đ}�`�F
��̓_���Ƃ���A�_B�́A�_P�Ɋւ��Đ}�`�F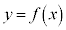 �ƑΏ̂Ȑ}�`��̓_�ł��B
�ƑΏ̂Ȑ}�`��̓_�ł��B
�Ƃ������Ƃ́A�A��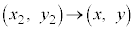 �Ƃ��āA�_P
�Ƃ��āA�_P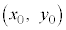 �Ɋւ��āA�������F
�Ɋւ��āA�������F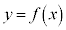 �ŕ\�����}�`�ƑΏ̂Ȑ}�`�̕������́A
�ŕ\�����}�`�ƑΏ̂Ȑ}�`�̕������́A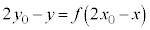
��1�D�_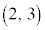 �Ɋւ��Ē����F
�Ɋւ��Ē����F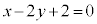 �ƑΏ̂Ȓ��������߂�B
�ƑΏ̂Ȓ��������߂�B
[��]�@���߂钼����̓_��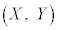 �Ƃ��Ē����F
�Ƃ��Ē����F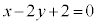 ����@ ��̓_
����@ ��̓_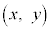 �́A
�́A
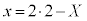 �C
�C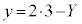
������A�@��x�Cy�ɑ������ƁA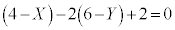
�������āA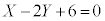
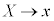 �C
�C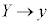 �Ə��������āA���߂钼���̎��́A
�Ə��������āA���߂钼���̎��́A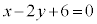 ......[��]
......[��]
���D�_�Ɋւ��đΏ̂ȕ������A���̑��̋Ȑ������߂�ꍇ���S�����l�ɂł��܂��B
 �����Ɋւ��đΏ̂Ȑ}�`
�����Ɋւ��đΏ̂Ȑ}�`
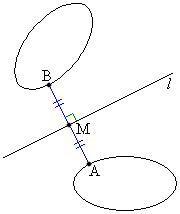
�_A�Ɠ_B������l�Ɋւ��đΏ�
�� (1) 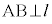 ���� (2) ����AB�̒��_M��l��
���� (2) ����AB�̒��_M��l��
�_A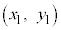 �Ɠ_B
�Ɠ_B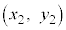 ���A�����F
���A�����F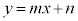 (
(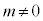 )�Ɋւ��đΏ�
)�Ɋւ��đΏ�
�� (1) 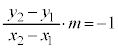 ���� (2)
���� (2) 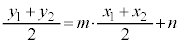
�_A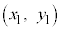 �Ɠ_B
�Ɠ_B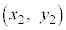 ���A�����F
���A�����F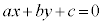 �Ɋւ��đΏ�
�Ɋւ��đΏ�
�� (1) 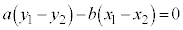 ���� (2)
���� (2) 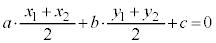
(�Ȃ��A2�����̕��s�E�������Q��)
�_A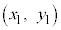 �Ɠ_B
�Ɠ_B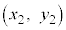 �����Ԓ����̌X���́A
�����Ԓ����̌X���́A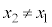 �ł���A
�ł���A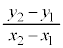
�����̕������́A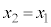 �̂Ƃ����܂߂āA
�̂Ƃ����܂߂āA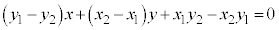
���̒����̖@���x�N�g���́A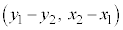
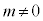 �ł����(
�ł����(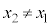 )�A
)�A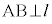 ��
�� 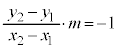
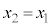 �̂Ƃ����܂߂āA
�̂Ƃ����܂߂āA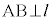 ��
�� 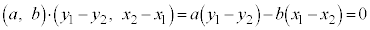
����AB�̒��_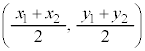 ������l��Ƃ��������́A����l�̕������ɁA
������l��Ƃ��������́A����l�̕������ɁA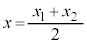 �C
�C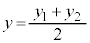 �����������𗧂Ă܂��B
�����������𗧂Ă܂��B
��2�D�����F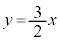 �Ɋւ��āA�����F
�Ɋւ��āA�����F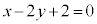 �ƑΏ̂Ȓ��������߂�B
�ƑΏ̂Ȓ��������߂�B
[��]�@ �����F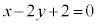 ����@ ��̓_��
����@ ��̓_��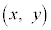 �C���߂钼����̓_��
�C���߂钼����̓_��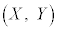 �Ƃ��܂��B
�Ƃ��܂��B
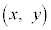 ��
��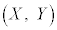 �������F
�������F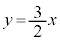 �Ɋւ��đΏ�
�Ɋւ��đΏ�
�� (1) 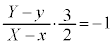 ���� (2)
���� (2) 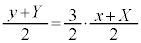
(1)���A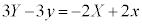
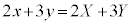 ����A
����A
(2)���A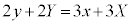
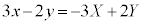 ����B
����B
�A�C�B��x�Cy�ɂ��ĉ����ƁA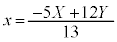 �C
�C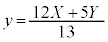
�@�ɑ�����āA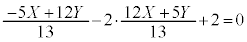
��������ƁA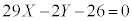
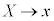 �C
�C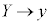 �Ƃ��āA���߂钼���̕������́A
�Ƃ��āA���߂钼���̕������́A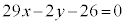 ......[��]
......[��]
���D�����Ɋւ��đΏ̂ȕ������A���̑��̋Ȑ������߂�ꍇ���S�����l�ɂł��܂��B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���w��b����TOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 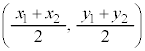 ������l��Ƃ��������́A����l�̕������ɁA
������l��Ƃ��������́A����l�̕������ɁA