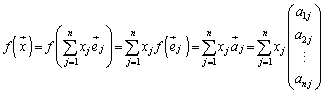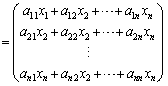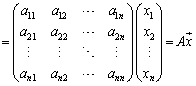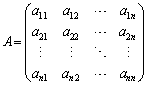1次変換 関連問題
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
この項目は、行列、ベクトルの1次独立を参照してください。
n次元ベクトル空間内の1次独立なn個のベクトルの組が、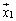 ,
,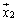 ,・・・,
,・・・,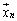 、及び、
、及び、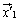 ,
,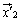 ,・・・,
,・・・,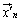 の2系統あるとします。
の2系統あるとします。
n次元ベクトル空間内の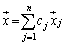 と、
と、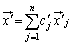 が1対1対応し、fという操作によって、
が1対1対応し、fという操作によって、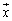 が
が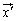 に対応するとき、fを変換と言い、
に対応するとき、fを変換と言い、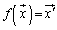 と表します。
と表します。
さらに、変換fが、任意の実数c,任意のベクトル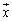 ,
,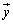 に対して、
に対して、
(i) 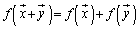
(ii) 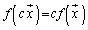
を満たす(この性質を線形性と言います)とき、fを1次変換と言います。
n次元ベクトル空間内のn個の単位ベクトルが互いに直交しているとき、この単位ベクトルの組を正規直交基底と言います。
正規直交基底として、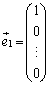 ,
,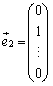 ,・・・,
,・・・,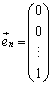 をとり、
をとり、
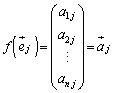 (
(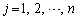 )とします。
)とします。
fが1次変換のときには、線形性(i),(ii)が成り立つので、n次元空間内の任意のベクトル: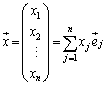 に対して、
に対して、
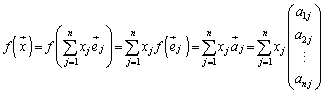
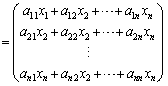
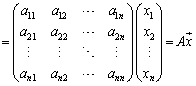
但し、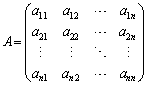
よって、1次変換fは行列を用いて記述できることがわかります。
また、逆に行列を用いて表せる変換は、線形性(i),(ii)を満たすので、1次変換です。
上記のように、行列は、もともと、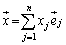 のように表されていたベクトルを、
のように表されていたベクトルを、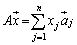 のように表現し直しているので、基底
のように表現し直しているので、基底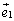 ,
,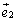 ,・・・,
,・・・,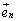 の組を基底
の組を基底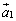 ,
,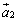 ,・・・,
,・・・,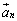 の組に入れ替えるという作業を行っているということがわかります。
の組に入れ替えるという作業を行っているということがわかります。
行列Aは、正規直交基底: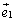 ,
,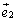 ,・・・,
,・・・,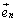 の1次変換fの行き先のベクトルを列ベクトルとして横に並べた形:
の1次変換fの行き先のベクトルを列ベクトルとして横に並べた形: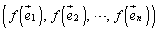 をしています。
をしています。
上記において、1次変換fに対して、行列Aのことを、1次変換fの表現行列と言います。また、行列Aに対して1次変換fを、行列Aが表現する1次変換、というような言い方をします。
単位行列Eの表す1次変換は、n次元座標空間内の点を自分自身に移すので、恒等変換と言います。
2次元座標平面における1次変換の代表的な例として、以下の変換があげられます。
(1) x軸に関する対称移動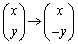 :表現行列は
:表現行列は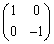
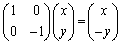
(2) y軸に関する対称移動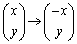 :表現行列は
:表現行列は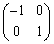
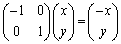
(3) 原点に関する対称移動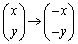 :表現行列は
:表現行列は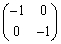
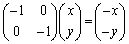
(4) 直線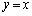 に関する対称移動
に関する対称移動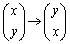 :表現行列は
:表現行列は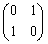
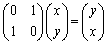
(1次変換(その2)へつづく)
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
数学基礎事項TOP 数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 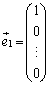 ,
,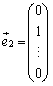 ,・・・,
,・・・,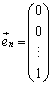 をとり、
をとり、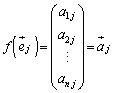 (
(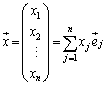 に対して、
に対して、