�����~�^���@�@�@�֘A���
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
����m�̕��̂����ar�̉~�������������v�Ŏ���^������Ƃ��A���̉^���������~�^���ƌ����B
�~�̒��S���畨�̂Ɍ������x�N�g��(���a�x�N�g���ƌ���)���A�P�ʎ���(1�b)������ɒʉ߂��镔���ɂł����`�̒��S�p���p���x�ƌ����B
�����~�^���́A�p���x���̉^���ƌ������Ƃ��ł���B
�����~�^�����镨�̂��p���x��ω �C�����x�̑傫����a�Ƃ���ƁA
����������B
�����~�^�����镨�̂ɂ́A�˂����S�Ɍ��������̑傫���̗��������B���̗͂����S���ƌ����B�����͂̑傫����F�Ƃ���ƁA�����~�^�����镨�̂��^��������(�@������)�́A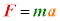 ��a�ɁA
��a�ɁA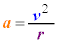 �܂��́A
�܂��́A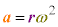 �������āA
�������āA
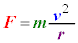 �C�܂��́A �C�܂��́A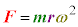 |
�P�ʎ���(1�b)�ɉ~�����������邩�𐔂�������]���Ƃ����B��]��n�́A
����@�~�̒��S�����_�Ƃ���xy���ʏ�ŕ��̂������~�^�����Ă���Ƃ��܂��B
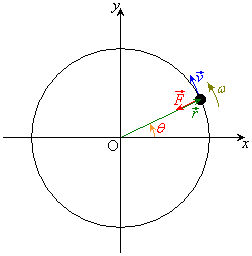 ���a�x�N�g����x�����甽���v�����pθ �̂Ƃ���ɂ���Ƃ��܂��B����
���a�x�N�g����x�����甽���v�����pθ �̂Ƃ���ɂ���Ƃ��܂��B����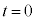 �ɓ��a�x�N�g����x���ƂȂ��p��δ �Ƃ��āA
�ɓ��a�x�N�g����x���ƂȂ��p��δ �Ƃ��āA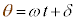 �ł��B
�ł��B
���̂����W��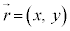 �Ƃ��āA
�Ƃ��āA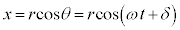 �C
�C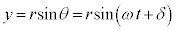 ����@
����@
���̂����x��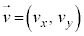 �Ƃ��āA
�Ƃ��āA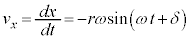 �C
�C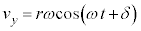 ����A
����A
���̂������x��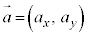 �Ƃ��āA
�Ƃ��āA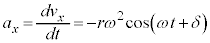 �C
�C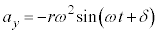 ����B
����B
�@�ƇB������ׂ�ƁA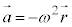
������A�����~�^�����Ă��镨�̂������x�́A���a�x�N�g��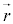 �Ƌt���������̂̈ʒu����~�̒��S�������Ă������Ƃ��킩��܂��B
�Ƌt���������̂̈ʒu����~�̒��S�������Ă������Ƃ��킩��܂��B
�����x�̑傫��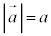 �́A
�́A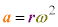 ����C
����C
�܂��A����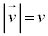 �́A�A���A
�́A�A���A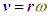 ����D
����D
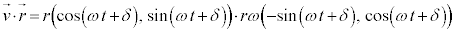
�� 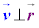
�܂�A�����~�^�����镨�̂����x�͓��a�x�N�g���Ɛ����ŁA�~���ڐ��̕����������܂��B
�C�C�D���Aω ����������ƁA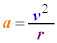
�����~�^�����镨�̂ɓ�����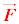 �́A�^�����������A
�́A�^�����������A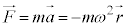 �ƂȂ�A���̂̈ʒu����~�̒��S�Ɍ����������ł��B���S�Ɍ������͂Ȃ̂Ō��S�͂ƌ����܂��B�^�����������~�̐ڐ������Ɩ@�������ɕ�����ƁA�ڐ������ɂ͑������ŗ͂��������A�����x������0�ł����A�@�������ɂ��ẮA
�ƂȂ�A���̂̈ʒu����~�̒��S�Ɍ����������ł��B���S�Ɍ������͂Ȃ̂Ō��S�͂ƌ����܂��B�^�����������~�̐ڐ������Ɩ@�������ɕ�����ƁA�ڐ������ɂ͑������ŗ͂��������A�����x������0�ł����A�@�������ɂ��ẮA
�Ƃ��������������܂��B�u���S�͂̑傫����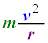 �ɓ������v�Ƃ������ƂɂȂ�܂��B
�ɓ������v�Ƃ������ƂɂȂ�܂��B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@������b����TOP�@�@����TOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B