変位・速度・加速度 関連問題
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
時刻tにおける物体の位置が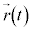 のとき、物体の速度は、
のとき、物体の速度は、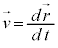 ,加速度は、
,加速度は、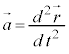
また、加速度が時間の関数として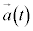 と与えられているとき、時刻
と与えられているとき、時刻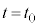 における速度(初速度)を
における速度(初速度)を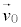 として、時刻tにおける速度
として、時刻tにおける速度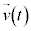 は、
は、
時刻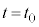 における位置を
における位置を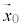 として、時刻tにおける位置
として、時刻tにおける位置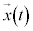 は、
は、
解説 運動する物体Pの時刻tにおける位置が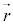 で表されるとします。
で表されるとします。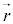 の成分は時刻tの関数になります。
の成分は時刻tの関数になります。
以下、簡単のために、Pがxy平面上を運動するものとして、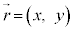 とします。
とします。
Pが時間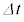 の間に、x方向に
の間に、x方向に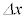 ,y方向に
,y方向に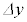 動くとすると、時刻
動くとすると、時刻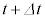 におけるPの位置は
におけるPの位置は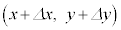 です。
です。
この間のPの位置の変化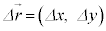 を変位と言います。
を変位と言います。
変位の単位は、位置、距離と同じく[m]です。
単位時間(1秒)あたりにどれくらい移動するかということで、物体の移動する速度を考えることができます。
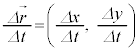 を平均速度と言います(平均変化率を参照)。これの大小により、
を平均速度と言います(平均変化率を参照)。これの大小により、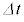 の間の物体の移動について、速いか遅いかを考えることができます。
の間の物体の移動について、速いか遅いかを考えることができます。
平均速度の単位は、距離を時間で割った[m/s]です。
例1 3秒間にx方向に12m,y方向に21m進む物体があるとする。この物体の平均速度は、x成分が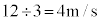 ,y成分が
,y成分が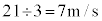 より、
より、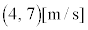 です。
です。
刻々と速度が変化するような物体の場合、平均速度だけでは、速いか遅いかを正確に扱うことができません。
そこで、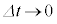 とした極限を考えるのです。この極限操作を行った時間を微小時間と言います。
とした極限を考えるのです。この極限操作を行った時間を微小時間と言います。
平均速度の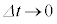 としたときの極限
としたときの極限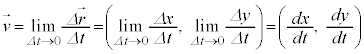 を速度と言います。速度は、各瞬間で移動の割合を考えたものです(微分・導関数を参照)。
を速度と言います。速度は、各瞬間で移動の割合を考えたものです(微分・導関数を参照)。
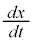 ,
,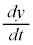 は、時刻tの関数
は、時刻tの関数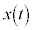 ,
,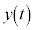 を時刻tで微分したもの(導関数)を表します。速度は変位を時間で微分したものです。
を時刻tで微分したもの(導関数)を表します。速度は変位を時間で微分したものです。
速度はベクトルですが、速度ベクトル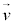 の大きさ
の大きさ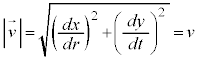 を速さと言います(根号部分は、曲線の長さの公式に出てくる形です)。
を速さと言います(根号部分は、曲線の長さの公式に出てくる形です)。
速度の単位は、平均速度と同じく、[m/s]です。
Pの速度が時間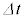 の間に
の間に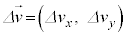 変化したとします。微小時間における速度変化、つまり、
変化したとします。微小時間における速度変化、つまり、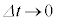 としたときの速度変化の極限
としたときの速度変化の極限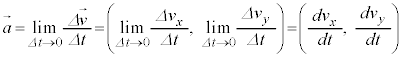 を加速度と言います。
を加速度と言います。
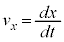 ,
,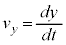 より、
より、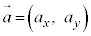 として、
として、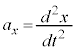 ,
,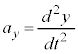 です。
です。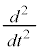 はtで2回微分することを表します。
はtで2回微分することを表します。
この記号を使って、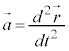 と書くことにします。加速度は、速度を時間で微分したものであり、変位を時間で2回微分したものです。
と書くことにします。加速度は、速度を時間で微分したものであり、変位を時間で2回微分したものです。
加速度の単位は、速度を時間で割ったものになり、[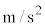 ]です。
]です。
例2 時刻tにおける物体Pの座標が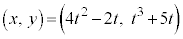 と表されるとき、
と表されるとき、
1次元の運動の場合、物体がx軸に沿って運動し、時刻tにおける加速度が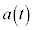 ,時刻
,時刻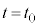 における速度が
における速度が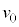 だとして、時刻tにおける速度
だとして、時刻tにおける速度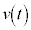 は、
は、
となりますが、定積分は面積を表す(定積分と面積を参照)ので、a−tグラフの面積は速度変化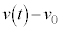 を表す、と言うこともできます。
を表す、と言うこともできます。
また、時刻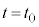 におけるx座標が
におけるx座標が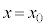 だとして、時刻tにおけるx座標
だとして、時刻tにおけるx座標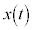 は、
は、
となりますが、v−tグラフの面積は変位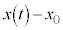 を表す、と言うこともできます。
を表す、と言うこともできます。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
物理基礎事項TOP 物理TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 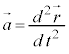
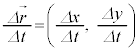 を平均速度と言います(平均変化率を参照)。これの大小により、
を平均速度と言います(平均変化率を参照)。これの大小により、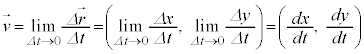 を速度と言います。速度は、各瞬間で移動の割合を考えたものです(微分・導関数を参照)。
を速度と言います。速度は、各瞬間で移動の割合を考えたものです(微分・導関数を参照)。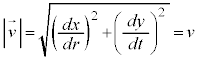 を速さと言います(根号部分は、曲線の長さの公式に出てくる形です)。
を速さと言います(根号部分は、曲線の長さの公式に出てくる形です)。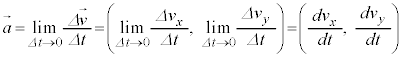 を加速度と言います。
を加速度と言います。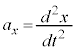 ,
,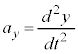 です。
です。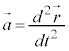 と書くことにします。加速度は、速度を時間で微分したものであり、変位を時間で2回微分したものです。
と書くことにします。加速度は、速度を時間で微分したものであり、変位を時間で2回微分したものです。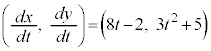 です。
です。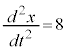 ,
,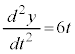 より、Pの加速度は、
より、Pの加速度は、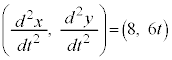 です。
です。