相変化
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
気体分子の大きさ、気体分子間に働く力を考慮した実在気体nモルの状態方程式は、圧力をp,体積をV,温度をT,気体定数をRとして、
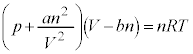 (a,bは定数) ・・・①
(a,bは定数) ・・・①
理想気体では、気体分子の大きさと気体分子間の力を無視して、状態方程式: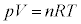 を考えていましたが、実際の気体では、気体分子の大きさ、気体分子間に働く力を考慮した状態方程式を考える必要があります。1873年、ファン・デル・ワールスにより提唱された実在気体の状態方程式が①です。
を考えていましたが、実際の気体では、気体分子の大きさ、気体分子間に働く力を考慮した状態方程式を考える必要があります。1873年、ファン・デル・ワールスにより提唱された実在気体の状態方程式が①です。
①の定数aは、分子間力の影響を表し、定数bは、1モルの気体分子が占有する体積に相当し、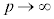 としたときの1モルの気体の体積Vの極限になっています。
としたときの1モルの気体の体積Vの極限になっています。
 気体1モル(水素を想定しています。
気体1モル(水素を想定しています。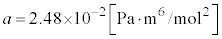 ,
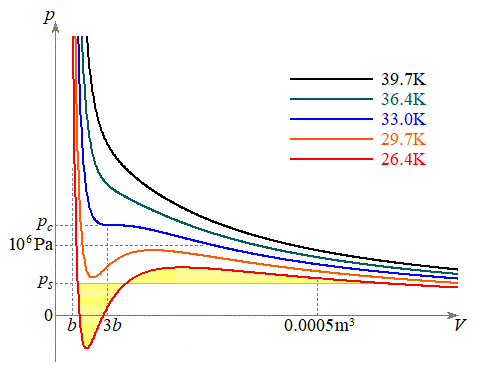
,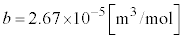 )として、ファンデルワールスの状態方程式のp-V図を5通りの温度について右図に示します。
)として、ファンデルワールスの状態方程式のp-V図を5通りの温度について右図に示します。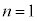 として、①は、
として、①は、
p-V図②は、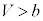 にのみ存在し、
にのみ存在し、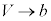 のとき
のとき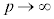 となります。温度がある程度高いとき、また、
となります。温度がある程度高いとき、また、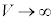 のときに、①のa,bの効果は小さくなり、p-V図②は理想気体のp-V図に近づいていきます。温度が下がって限界値
のときに、①のa,bの効果は小さくなり、p-V図②は理想気体のp-V図に近づいていきます。温度が下がって限界値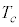 になると、p-V図②は停留点をもち、さらに温度が下がると、p-V図②は極小と極大を持つようになります。このとき、体積が大きく理想気体に近い状態から体積をだんだん小さくしていくと次第に圧力が大きくなりますが、圧力が気体の飽和蒸気圧
になると、p-V図②は停留点をもち、さらに温度が下がると、p-V図②は極小と極大を持つようになります。このとき、体積が大きく理想気体に近い状態から体積をだんだん小さくしていくと次第に圧力が大きくなりますが、圧力が気体の飽和蒸気圧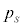 (気体の温度によって変わります)に達すると、それ以上圧力は高くなることができず、気体が液化し始め、以後、圧力は
(気体の温度によって変わります)に達すると、それ以上圧力は高くなることができず、気体が液化し始め、以後、圧力は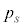 で一定のまま、液化が進むとともに体積が小さくなっていきます(右図の赤線、
で一定のまま、液化が進むとともに体積が小さくなっていきます(右図の赤線、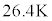 の場合において、圧力一定の線分をピンク色で描いてあります。この線分とp-V図②とで囲む2つの部分、図で薄黄色に着色されている部分の面積は等しくなることが知られています)。気体がすべて液体になってしまうと,液体のままp-V図②に沿って圧力が高くなって行きます。
の場合において、圧力一定の線分をピンク色で描いてあります。この線分とp-V図②とで囲む2つの部分、図で薄黄色に着色されている部分の面積は等しくなることが知られています)。気体がすべて液体になってしまうと,液体のままp-V図②に沿って圧力が高くなって行きます。
温度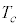 は液化が起こる限界の温度で臨界温度(水素では
は液化が起こる限界の温度で臨界温度(水素では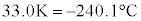 )と言います。
)と言います。
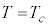 のとき、p-V図②が停留点(このときの体積を
のとき、p-V図②が停留点(このときの体積を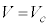 とします)をもつので、
とします)をもつので、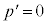 と
と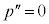 が共通解
が共通解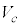 を持ちます。
を持ちます。
②のpをVの関数としてVで微分すると、
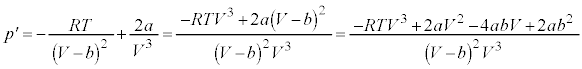 ・・・③
・・・③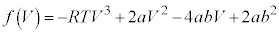 とおくと、
とおくと、
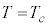 のとき、
のとき、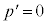 と
と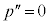 が
が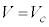 を共通解に持つので、
を共通解に持つので、
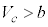 より
より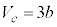
∴ 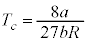
このとき、
よって、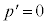
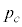 を臨界圧力(水素では
を臨界圧力(水素では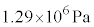 )と言います。
)と言います。
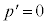 のとき、③より、
のとき、③より、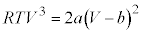 となり、
となり、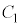 :
: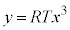 と
と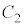 :
: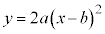 のグラフの共有点を考えることになります。上記の考察より、
のグラフの共有点を考えることになります。上記の考察より、
・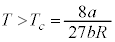 のとき、
のとき、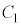 と
と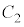 は
は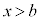 において
において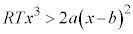 であって共有点を持ちません。即ち、
であって共有点を持ちません。即ち、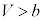 において
において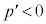 であり、p-V図②(右図の黒線、緑線の場合)は、単調減少で、気体は液化しません。
であり、p-V図②(右図の黒線、緑線の場合)は、単調減少で、気体は液化しません。 ・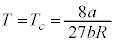 のとき、
のとき、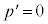 と
と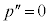 が
が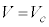 を共通解に持つので、
を共通解に持つので、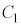 と
と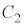 は
は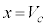 において接します。
において接します。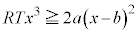 で等号は
で等号は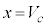 のときのみです。p-V図②は、
のときのみです。p-V図②は、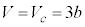 に停留点
に停留点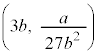 をもち、他では単調減少です。
をもち、他では単調減少です。 ・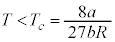 のとき、④を考慮すると3次方程式
のとき、④を考慮すると3次方程式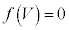 は3個の解を持ち、そのうちの1個は
は3個の解を持ち、そのうちの1個は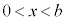 の範囲にありますが、
の範囲にありますが、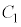 と
と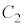 は
は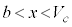 に1交点(
に1交点(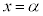 とします。
とします。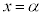 は
は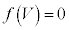 の解です)、
の解です)、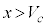 に1交点(
に1交点(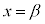 とします。
とします。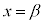 は
は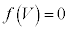 の解です)を持ちます。
の解です)を持ちます。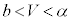 では
では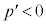 でp-V図②は減少、
でp-V図②は減少、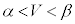 では
では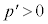 でp-V図②は増加、
でp-V図②は増加、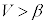 では
では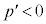 でp-V図②は減少です。このときは、前述したように、気体の体積を小さくしていき、気体の圧力が飽和蒸気圧に達した段階で、p-V図②から離れて、気体は液化を始め、気体が全て液体になるまで気体の圧力は飽和蒸気圧で一定になります。
でp-V図②は減少です。このときは、前述したように、気体の体積を小さくしていき、気体の圧力が飽和蒸気圧に達した段階で、p-V図②から離れて、気体は液化を始め、気体が全て液体になるまで気体の圧力は飽和蒸気圧で一定になります。 こうして右上のグラフが得られます。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
物理基礎事項TOP 物理TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 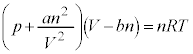 (a,bは定数) ・・・①
(a,bは定数) ・・・①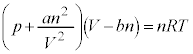 (a,bは定数) ・・・①
(a,bは定数) ・・・①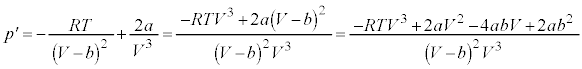 ・・・③
・・・③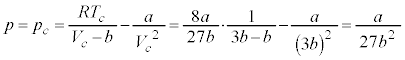
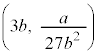 をもち、他では単調減少です。
をもち、他では単調減少です。