������w2012�N�O�������������
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
[1]�@���፷��h�̐�����H�Ɛ�����L�̊ԂɂȂ߂炩�ȎΖʂ�����A���������̒f�ʂ͐}1-1�̂悤�ɂȂ��Ă���B������L�̓��[�ɂ͓�k�ɂ̂т鉔���ȕǂ�����B�����ŏ����̏Փˎ������s�����B���ׂĂ̏����͖ʂ��痣��邱�ƂȂ��i�݁A�݂��ɒe���Փ˂�����̂Ƃ��A�����ƕǂ��e���Փ˂�����̂Ƃ���B�d�͉����x�̑傫����g�Ƃ��A�����̑傫�����]�A���C���C��R�͖������Ĉȉ��̐ݖ�ɓ�����B
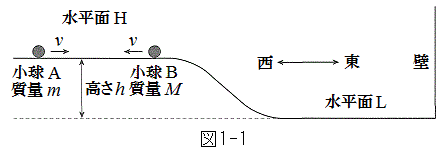
�T�@�}1-1�̂悤�ɁA������H�Ŏ���m�̏���A�𓌌����ɑ���v�Ŋ��点�A����M�̏���B�𐼌����ɑ���v�Ŋ��点�ďՓ˂������Ƃ���A�Փˌ�ɏ���A�͐������ɐi�݁A����B�͐Î~�����B
(1) �Փˌ�̏���A�̑��������߂�B
(2) ���ʂ̔�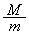 �����߂�B
�����߂�B
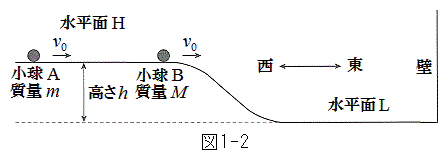
�U�@�}1-2�̂悤�ɁA������H�őO��̏���A�Ə���B�𓌌����ɓ�������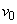 �Ŋ��点���Ƃ���A����B�͕ǂŒ��˕Ԃ�A������L����̍�����x�̎Ζʏ�̓_�ŏ���A�ƏՓ˂����B���̌�A����A�͎Ζʂ��オ���Đ�����H��̍ŏ��̈ʒu�𑬂�
�Ŋ��点���Ƃ���A����B�͕ǂŒ��˕Ԃ�A������L����̍�����x�̎Ζʏ�̓_�ŏ���A�ƏՓ˂����B���̌�A����A�͎Ζʂ��オ���Đ�����H��̍ŏ��̈ʒu�𑬂�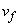 �Ő������ɒʉ߂��A����A����B�͕ǂƎΖʂ̊Ԃ������^�������B
�Ő������ɒʉ߂��A����A����B�͕ǂƎΖʂ̊Ԃ������^�������B
(1) 2�̏������Փ˂��钼�O�̏���A�̑�����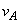 �C����B�̑�����
�C����B�̑�����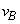 �Ƃ���B�����̔�
�Ƃ���B�����̔�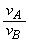 �����߂�B
�����߂�B
(2) x��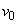 �C
�C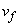 �Ch�Cg��p���ĕ\���B
�Ch�Cg��p���ĕ\���B �V�@�O��̏���B���A������L���獂��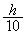 �̒n�_�ƕǂƂ̊Ԃ𓌐������ɉ����^�����Ă���Ƃ��A�}1-3�̂悤�ɏ���B���˂���Ď���
�̒n�_�ƕǂƂ̊Ԃ𓌐������ɉ����^�����Ă���Ƃ��A�}1-3�̂悤�ɏ���B���˂���Ď���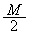 �̏���C�𐅕���H��̓_���甭�˂����B������L��ŏ���C�͂��܂�����B�ɖ������A���̌㏬��B���ǂŒ��˕Ԃ��Ă���A����C�Ə���B�������Ƃ�������H�܂ŏオ���Ă����B2�̏����͓�������
�̏���C�𐅕���H��̓_���甭�˂����B������L��ŏ���C�͂��܂�����B�ɖ������A���̌㏬��B���ǂŒ��˕Ԃ��Ă���A����C�Ə���B�������Ƃ�������H�܂ŏオ���Ă����B2�̏����͓�������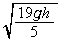 �ŋ�����
�ŋ����� �ɕۂ����܂ܐ�����H��������ɐi�B���̕����͐�����k�Ɍ����Ă̊p�x��α�Ƃ����
�ɕۂ����܂ܐ�����H��������ɐi�B���̕����͐�����k�Ɍ����Ă̊p�x��α�Ƃ����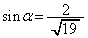 �ł������B
�ł������B (1) �ǂŒ��˕Ԃ������Ƃ̏���B�̐�����L�ł̉^���̖��@�́A������k�Ɍ����Ċp�xβ �ł������B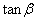 �����߂�B
�����߂�B (2) ����B�Ə���C���Փ˂����n�_�̕ǂ���̋���d�����߂�B
(3) ������H��Ŕ��˂����Ƃ��̏���C�̑���V�����߂�B
(4) ����C�˂��������𓌂���k�Ɍ����Ċp�xθ �Ƃ���B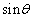 �����߂�B
�����߂�B [��]
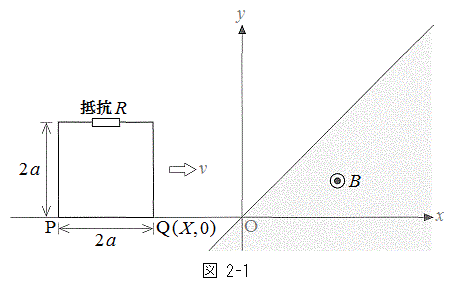 [2]�@�}2-1�̂悤�ɁAxy���ʏ�ɒu���ꂽ�c���̒������Ƃ���
[2]�@�}2-1�̂悤�ɁAxy���ʏ�ɒu���ꂽ�c���̒������Ƃ��� �̉�H�����̑���v��x���������ɓ������B��H�̍����̓_P�ƉE���̓_Q�͏��x����ɂ���A�_Q�̍��W��
�̉�H�����̑���v��x���������ɓ������B��H�̍����̓_P�ƉE���̓_Q�͏��x����ɂ���A�_Q�̍��W��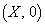 �Ƃ���B�������xB�̈�l�Ȏ��ꂪ�A
�Ƃ���B�������xB�̈�l�Ȏ��ꂪ�A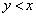 �̗̈�ɂ̂ݎ��ʂɐ����ɂ������Ă���B�����̑����A��R����уR���f���T�[�̑f�q�̑傫���A�����̒�R����щ�H�𗬂��d������鎥��̉e���͖����ł�����̂Ƃ��āA�ȉ��̐ݖ�ɓ�����B
�̗̈�ɂ̂ݎ��ʂɐ����ɂ������Ă���B�����̑����A��R����уR���f���T�[�̑f�q�̑傫���A�����̒�R����щ�H�𗬂��d������鎥��̉e���͖����ł�����̂Ƃ��āA�ȉ��̐ݖ�ɓ�����B
�T�@�܂��A�}2-1�Ɏ�������R�lR�̒�R�Ɠ�������Ȃ鐳���`�̉�H��p����B
(1) 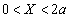 �̂Ƃ��ɉ�H�𗬂��d���̑傫�������߂�B
�̂Ƃ��ɉ�H�𗬂��d���̑傫�������߂�B (2) 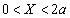 �̂Ƃ��ɉ�H�����ꂩ���͂�x���������߂�B
�̂Ƃ��ɉ�H�����ꂩ���͂�x���������߂�B (3) 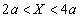 �̂Ƃ��ɉ�H�����ꂩ���͂�x���������߂�B
�̂Ƃ��ɉ�H�����ꂩ���͂�x���������߂�B �U�@���ɁA�ݖ�T�ŗp������H���̒�R���܂މ�H�Ɏ��ւ���B
(1) �}2-2�Ɏ�������R�lR�̒�R��2�܂މ�H��p�����ꍇ�ɑ��āA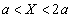 �̂Ƃ���PQ�Ԃ̓����𗬂��d���̑傫�������߂�B
�̂Ƃ���PQ�Ԃ̓����𗬂��d���̑傫�������߂�B (2) �}2-3�Ɏ�������R�lR�̒�R��3�܂މ�H��p�����ꍇ�ɑ��āA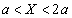 �̂Ƃ���PQ�Ԃ̒�R�𗬂��d���̑傫�������߂�B
�̂Ƃ���PQ�Ԃ̒�R�𗬂��d���̑傫�������߂�B
�V�@�Ō�ɁA�}2-4�Ɏ������d�C�e��C�̃R���f���T�[�Ɠ�������Ȃ��H��p����B
(1) 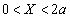 �̂Ƃ��ɓ����𗬂��d���̑傫�������߂�B
�̂Ƃ��ɓ����𗬂��d���̑傫�������߂�B (2) 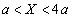 �̂Ƃ��ɉ�H�����ꂩ���͂�x���������߂�B
�̂Ƃ��ɉ�H�����ꂩ���͂�x���������߂�B [��]
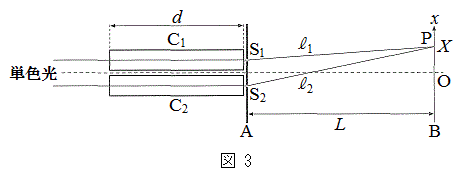 [3]�@���X���b�g�ɂ����̊��𗘗p���ċC�̂̋��ܗ��𑪒肷������ɂ��čl���悤�B�}3�̂悤�ɁA�����ȓ�̖��e��
[3]�@���X���b�g�ɂ����̊��𗘗p���ċC�̂̋��ܗ��𑪒肷������ɂ��čl���悤�B�}3�̂悤�ɁA�����ȓ�̖��e��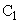 �C
�C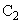 (����d)���A����A��ɂ����̃X���b�g
(����d)���A����A��ɂ����̃X���b�g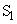 �C
�C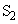 (�X���b�g�Ԋua)�̒��O�ɒu���AA�̌���ɂ̓X�N���[��B��z�u����BA�CB�݂͌��ɕ��s�ł���A���̊Ԃ̋�����L�Ƃ���B�X�N���[��B��̍��W��x���AO�����_�Ƃ��Đ}3�̂悤�ɂƂ�B���_O��
(�X���b�g�Ԋua)�̒��O�ɒu���AA�̌���ɂ̓X�N���[��B��z�u����BA�CB�݂͌��ɕ��s�ł���A���̊Ԃ̋�����L�Ƃ���B�X�N���[��B��̍��W��x���AO�����_�Ƃ��Đ}3�̂悤�ɂƂ�B���_O��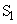 �C
�C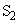 ���瓙�����ɂ���B���܁A���ʔg�ƌ��Ȃ���P�F��(�g��λ)���A���e���ʂ��ăX���b�g�ɐ����ɏƎ˂���ƁA�X�N���[��B��ɂ͑����̊��Ȃ������B���e��̕ǂ̌����͖������āA�ȉ��̐ݖ�ɓ�����B
���瓙�����ɂ���B���܁A���ʔg�ƌ��Ȃ���P�F��(�g��λ)���A���e���ʂ��ăX���b�g�ɐ����ɏƎ˂���ƁA�X�N���[��B��ɂ͑����̊��Ȃ������B���e��̕ǂ̌����͖������āA�ȉ��̐ݖ�ɓ�����B
�T�@���e��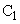 �C
�C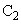 �����̓����ɐ^��ɂ����ꍇ�A���������̃X���b�g
�����̓����ɐ^��ɂ����ꍇ�A���������̃X���b�g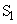 �C
�C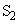 �܂ł̌��H���͓��������߁A�P�F����
�܂ł̌��H���͓��������߁A�P�F����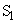 �C
�C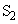 �ɂ����ē��ʑ��ł���B
�ɂ����ē��ʑ��ł���B (1) �X�N���[��B��̓_P��x���W��X�C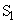 ��P�̋�����
��P�̋�����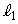 �C
�C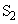 ��P�̋�����
��P�̋�����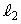 �Ƃ����Ƃ��A�����̍�
�Ƃ����Ƃ��A�����̍�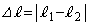 ���Aa�C
���Aa�C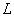 �CX��p���ĕ\���B�������AL��a��
�CX��p���ĕ\���B�������AL��a��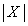 �����\���ɑ傫�����̂Ƃ���B�Ȃ��A
�����\���ɑ傫�����̂Ƃ���B�Ȃ��A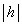 ��1�����\����������A
��1�����\����������A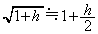 �Ƌߎ��ł��邱�Ƃ𗘗p���Ă悢�B
�Ƌߎ��ł��邱�Ƃ𗘗p���Ă悢�B (2) �_P�ɖ���������Ƃ��AX��a�CL�Cλ�C����ѐ���m��p���ĕ\���B
�U�@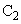 �̗e�����^��ɕۂ����܂܁A
�̗e�����^��ɕۂ����܂܁A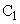 �̗e����ɋC�̂��������Ɠ���͂��߂��B��ʂɐ�Ή��xT�C����p�̋C�̂̋��ܗ��Ɛ^��̋��ܗ��Ƃ̍��́A���̋C�̂̐����x(�P�ʑ̐ς�����̋C�̕��q�̐�)ρ�ɔ�Ⴗ��B
�̗e����ɋC�̂��������Ɠ���͂��߂��B��ʂɐ�Ή��xT�C����p�̋C�̂̋��ܗ��Ɛ^��̋��ܗ��Ƃ̍��́A���̋C�̂̐����x(�P�ʑ̐ς�����̋C�̕��q�̐�)ρ�ɔ�Ⴗ��B (1) �e����̋C�̂̈��͂�p�Ő�Ή��x��T�̂Ƃ��A���̋C�̂̐����xρ��p�CT�Ck (�{���c�}���萔)��p���ĕ\���B�������A���̋C�̂͗��z�C�̂Ƃ݂Ȃ��Ă悢�B
(2) ���x�����ɕۂ����܂�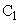 �̗e����ɋC�̂����Ĉ��͂��グ��ƁA�X�N���[��B��̊��Ȃ́Ax���̐������A�������̂ǂ���Ɉړ����邩�B���R�����ē�����B
�̗e����ɋC�̂����Ĉ��͂��グ��ƁA�X�N���[��B��̊��Ȃ́Ax���̐������A�������̂ǂ���Ɉړ����邩�B���R�����ē�����B
�V�@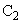 �̗e�����^��ɕۂ����܂܁A
�̗e�����^��ɕۂ����܂܁A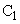 �̗e����Ή��xT�C1�C��(101.3kPa)�̋C�̂Ŗ��������B���̂Ƃ��̋C�̂̋��ܗ���n�Ƃ���B
�̗e����Ή��xT�C1�C��(101.3kPa)�̋C�̂Ŗ��������B���̂Ƃ��̋C�̂̋��ܗ���n�Ƃ���B (1) 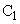 �̗e�킪�^���Ԃ����Ή��xT�C1�C���̋C�̂Ŗ��������܂łɁA���ꂼ��̖����̓X�N���[��B�������
�̗e�킪�^���Ԃ����Ή��xT�C1�C���̋C�̂Ŗ��������܂łɁA���ꂼ��̖����̓X�N���[��B�������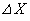 �����ړ������B�C�̂̋��ܗ�n���A
�����ړ������B�C�̂̋��ܗ�n���A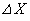 ��p���ĕ\���B
��p���ĕ\���B (2) (1)�ŁA���_O��N�{�̈Ð����ʉ߂�����A���������_O�ɗ��Ď~�܂����B�C�̂̋��ܗ�n���AN��p���ĕ\���B
[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���啨��TOP�@�@����TOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B