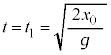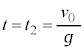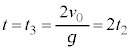�������x�^���@�@�@�֘A���
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
(���̍��ڂ́A�ψʁE���x�E�����x�̍��ڂ��Q�Ƃ��Ă�������)
���̂��꒼��������̉����x�ʼn^������Ƃ��A���̉^�����������x�^���ƌ����B���̂ɓ����͂�����ł���Ƃ��ɁA���͓̂������x�^�����s���B
��������xa���������x�^�����镨�̂��^�����������x���A����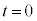 �ɕ��̂����W
�ɕ��̂����W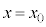 �Ɉʒu���āA���x
�Ɉʒu���āA���x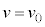 �ł������Ƃ���ƁA����t�ɂ��������xv�C���Wx�́A
�ł������Ƃ���ƁA����t�ɂ��������xv�C���Wx�́A
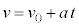 �@���(1)
�@���(1)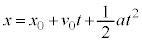 �@���(2)
�@���(2)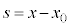 �Ƃ��āA
�Ƃ��āA
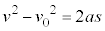 �@���(3)
�@���(3)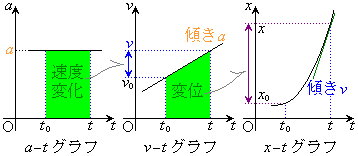 �������x�^���̖��������ۂɁA�ȉ��̎����𗘗p����ƕ֗��B
�������x�^���̖��������ۂɁA�ȉ��̎����𗘗p����ƕ֗��B
�����������A�c���������x���Ƃ��ĕ`�����O���t��a�|t�O���t�ƌ����Ba�|t�O���t�̖ʐς͑��x�ω��ɓ������B
�����������A�c�������x���Ƃ��ĕ`�����O���t��v�|t�O���t�ƌ����Bv�|t�O���t�̖ʐς͕ψʂɓ������B�܂��Av�|t�O���t�̌X���͉����x�ɓ������B
�����������A�c���ɕ��̂̈ʒu�������W���Ƃ��ĕ`�����O���t��x�|t�O���t�ƌ����Bx�|t�O���t�̐ڐ��̌X���͑��x�ɓ������B
����@1�����̕��̂̉^���ɂ����ẮA�^�����������x���C����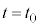 �ɂ����镨�̂����W��
�ɂ����镨�̂����W��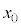 �C���̂����x��
�C���̂����x��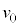 �C����t�ɂ����镨�̂����W��
�C����t�ɂ����镨�̂����W��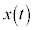 �C���x��
�C���x��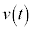 �C�����x��
�C�����x��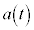 �Ƃ��āA
�Ƃ��āA
�����藧���܂�(�ψʁE���x�E�����x���Q��)�B
������Ax�������������xa�ʼn^�����镨�̂��A����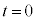 �ɂ����āA���W
�ɂ����āA���W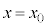 �Ɉʒu���āA���x
�Ɉʒu���āA���x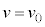 �ł������Ƃ���ƁA����t�ɂ��������xv�́A
�ł������Ƃ���ƁA����t�ɂ��������xv�́A
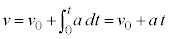 �@����@
�@����@
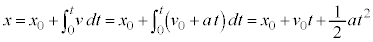 �@����A
�@����A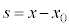 �Ƃ��āA
�Ƃ��āA
�� 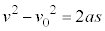
�ƂȂ�܂��B
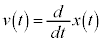 �Ƃ������Ƃ́Ax�|t�O���t(�������x�^���ł͕�����)�̐ڐ��̌X�������x���Ƃ������Ƃ��Ӗ����Ă��܂��B
�Ƃ������Ƃ́Ax�|t�O���t(�������x�^���ł͕�����)�̐ڐ��̌X�������x���Ƃ������Ƃ��Ӗ����Ă��܂��B
�܂��A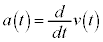 �Ƃ������Ƃ́Av�|t�O���t�̐ڐ��̌X���������x���Ƃ������Ƃ��Ӗ����Ă��܂��B
�Ƃ������Ƃ́Av�|t�O���t�̐ڐ��̌X���������x���Ƃ������Ƃ��Ӗ����Ă��܂��B
�������x�^���ł́Av�|t�O���t�͒����ł���A���̒����̌X���������x�ł��B
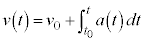 �́Aa�|t�O���t������
�́Aa�|t�O���t������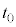 �������t�܂ł̖ʐς��A���x�ω��F
�������t�܂ł̖ʐς��A���x�ω��F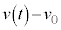 �ł��邱�Ƃ������Ă��܂��B
�ł��邱�Ƃ������Ă��܂��B
�������x�^���ł������x���Ȃ̂ŁAa�|t�O���t�͉����ɕ��s�Ȓ����ł���Aa�|t�O���t�Ɖ����ɋ��܂ꂽ�����`�̖ʐς����x�ω��ɂȂ�܂��B
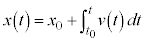 �́Av�|t�O���t������
�́Av�|t�O���t������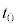 �������t�܂ł̖ʐς��A�ψ��F
�������t�܂ł̖ʐς��A�ψ��F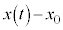 �ł��邱�Ƃ������Ă��܂��B
�ł��邱�Ƃ������Ă��܂��B
�������x�^���ł́Av�|t�O���t�͒����ł���Av�|t�O���t�Ɖ����ŋ��܂ꂽ��`�̖ʐς��ψ��ɂȂ�܂��B
�d�͉����x��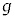 �Ƃ��āA���̂��n�\���d��
�Ƃ��āA���̂��n�\���d��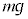 �ȊO�̗͂����ɉ^������Ƃ��������x�́A������������
�ȊO�̗͂����ɉ^������Ƃ��������x�́A������������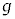 �ł��B�������x�^���ł́A����(1)�`(3)�͂�������o���܂��傤�B�ł����A�ȉ��̗�1�`��5�̌��ʂ܂ňËL���悤�Ƃ��Ă͂����܂���B�ËL�����o���ƕ����͓_�����Ȃ��Ȃ�܂��B���̏ɍ��킹�āA�����x�A���x�A�����x�̌������l�����ĕ��������߂�悤�ɂ��Ă��������B
�ł��B�������x�^���ł́A����(1)�`(3)�͂�������o���܂��傤�B�ł����A�ȉ��̗�1�`��5�̌��ʂ܂ňËL���悤�Ƃ��Ă͂����܂���B�ËL�����o���ƕ����͓_�����Ȃ��Ȃ�܂��B���̏ɍ��킹�āA�����x�A���x�A�����x�̌������l�����ĕ��������߂�悤�ɂ��Ă��������B
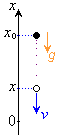 ��1�@���R�����F����
��1�@���R�����F����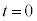 �ɂ����āA���̂����������������
�ɂ����āA���̂����������������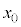 �̒n�_����Â��ɗ���������Ƃ��A����t�ɂ���������x�́A��L�̌���(1)�C(2)�ɂ����āA
�̒n�_����Â��ɗ���������Ƃ��A����t�ɂ���������x�́A��L�̌���(1)�C(2)�ɂ����āA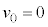 �C
�C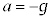 �Ƃ��āA
�Ƃ��āA
���̂�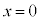 �̒n�_�܂ŗ�������̂ɗv��������
�̒n�_�܂ŗ�������̂ɗv��������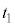 �́A
�́A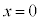 �Ƃ��āA
�Ƃ��āA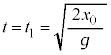
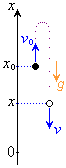 ��2�@������������F����
��2�@������������F����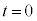 �ɂ����āA���̂����������������
�ɂ����āA���̂����������������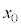 �̒n�_��������
�̒n�_��������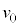 �œ����グ��Ƃ��A����t�ɂ���������x�́A��L�̌���(1)�C(2)�ɂ����āA
�œ����グ��Ƃ��A����t�ɂ���������x�́A��L�̌���(1)�C(2)�ɂ����āA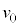 �͂��̂܂܁A
�͂��̂܂܁A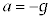 �Ƃ��āA
�Ƃ��āA
���̂��ō��_�ɒB����܂ł�����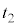 �́A�ō��_�ł�
�́A�ō��_�ł�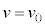 ���A
���A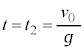
���̂������グ���n�_�ɖ߂��Ă���܂ł�����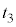 �́A
�́A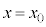 �Ƃ��āA
�Ƃ��āA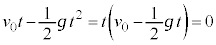 ���A
���A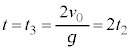
����������˂œ����グ�Ă���ō��_�܂ł̉^���ƁA�ō��_���瓊���グ�����_�ɖ߂��Ă���܂ł̉^���Ƃ́A�r�f�I�ŎB�e���ċt�ɂ����̂Ɠ����^���ɂȂ�܂��B����āA�^���̑Ώ̐����A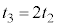 �ɂȂ�܂��B
�ɂȂ�܂��B
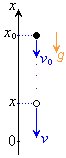 ��3�@�������������F����
��3�@�������������F����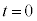 �ɂ����āA���̂�����������������
�ɂ����āA���̂�����������������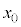 �̒n�_��������
�̒n�_��������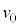 �œ������낷�Ƃ��A����t�ɂ���������x�́A��L�̌���(1)�C(2)�ɂ����āA
�œ������낷�Ƃ��A����t�ɂ���������x�́A��L�̌���(1)�C(2)�ɂ����āA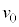 ��
��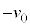 �ɑウ�A
�ɑウ�A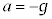 �Ƃ��āA
�Ƃ��āA
2�����̉^���ł́A���������Ɖ���������ʁX�ɍl���܂��B
�n�\���d���݂̂��镨�̂̉^���ł́A���������ɓ����x�^���A���������ɓ������x�^���ɂȂ�܂��B
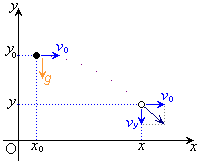 ��4�@���������F����������x���A���������ɏ������y�����Ƃ�܂��B����
��4�@���������F����������x���A���������ɏ������y�����Ƃ�܂��B����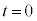 �ɂ����āA�ʒu
�ɂ����āA�ʒu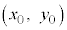 ���A���̂𐅕�����������
���A���̂𐅕�����������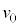 �œ�����Ƃ��A����t�ɂ��������x��
�œ�����Ƃ��A����t�ɂ��������x��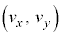 �C���W��
�C���W��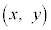 �Ƃ��܂��B
�Ƃ��܂��B
���������́A���R�����Ɠ����ŁA��L�̌���(1)�C(2)�ɂ����āA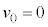 �C
�C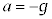 �Ƃ��āA
�Ƃ��āA
���������́A���x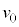 �̓����x�^���ŁA��L�̌���(1)�C(2)�ɂ����āA
�̓����x�^���ŁA��L�̌���(1)�C(2)�ɂ����āA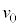 �͂��̂܂܁A
�͂��̂܂܁A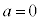 �Ƃ��āA
�Ƃ��āA
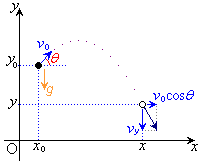 ��5�@�Ε������F����������x���A���������������y�����Ƃ�܂��B����
��5�@�Ε������F����������x���A���������������y�����Ƃ�܂��B����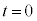 �ɂ����āA�ʒu
�ɂ����āA�ʒu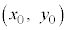 ���A���̂𐅕���������pθ ���������������
���A���̂𐅕���������pθ ���������������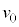 �œ����グ��Ƃ��A����t�ɂ��������x��
�œ����グ��Ƃ��A����t�ɂ��������x��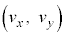 �C���W��
�C���W��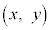 �Ƃ��܂��B
�Ƃ��܂��B
�����x�̐�������������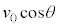 �C��������������
�C��������������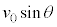 �ł��B
�ł��B
���������́A����������˂Ɠ����ŁA��L�̌���(1)�C(2)�ɂ����āA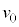 ��
��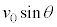 �ɑウ�A
�ɑウ�A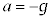 �Ƃ��āA
�Ƃ��āA
���������́A���x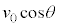 �̓����x�^���ł��B��L�̌���(1)�C(2)�ɂ����āA
�̓����x�^���ł��B��L�̌���(1)�C(2)�ɂ����āA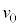 ��
��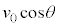 �ɑウ�A
�ɑウ�A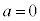 �Ƃ��āA
�Ƃ��āA
��L�̌���(3)�ɂ�����t���o�Ă��܂���B����(3)�́A����t���o�Ă��Ȃ��^���̂Ƃ��Ɏg���܂��B
��6�@��5�ɂ����āA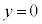 �ƂȂ�n�_�܂ŗ����Ƃ������x�̉���������
�ƂȂ�n�_�܂ŗ����Ƃ������x�̉���������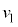 �Ƃ��܂��B����(3)�ɂ����āA
�Ƃ��܂��B����(3)�ɂ����āA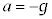 �C
�C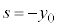 �Ƃ��āA
�Ƃ��āA
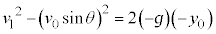 ��
�� 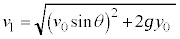
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@������b����TOP�@�@����TOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 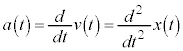 �C
�C