�����E�]���̉��@�藝�@�@�@�֘A���
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
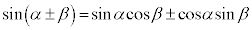 �@(��������)
�@(��������)
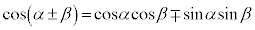 �@(��������)
�@(��������)
 [�ؖ�]�@���_O�𒆐S�Ƃ��锼�a1�̉~����ɉE�}�̂悤�ɁA2�_A
[�ؖ�]�@���_O�𒆐S�Ƃ��锼�a1�̉~����ɉE�}�̂悤�ɁA2�_A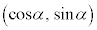 �CB
�CB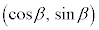 ���Ƃ�܂�(�����ł́A
���Ƃ�܂�(�����ł́A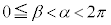 �Ƃ��܂�)�B
�Ƃ��܂�)�B
2�_A�CB�Ԃ̋�����2��́A
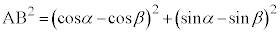
�@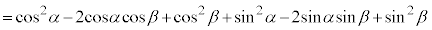
�@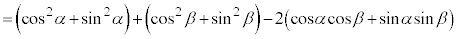
�@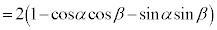 ����@
����@
����A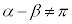 �̂Ƃ��A�O�p�`AOB�ɂ����āA�]���藝���A
�̂Ƃ��A�O�p�`AOB�ɂ����āA�]���藝���A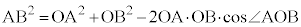 ����A
����A
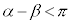 �̂Ƃ��́A
�̂Ƃ��́A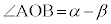 ���A
���A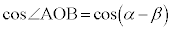
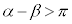 �̂Ƃ��́A
�̂Ƃ��́A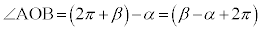 ���A
���A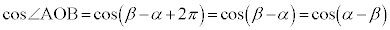
����āA�A�́A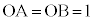 ���A
���A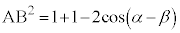 �@����B
�@����B
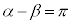 �̂Ƃ�(
�̂Ƃ�(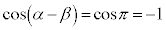 )�́AAB�͉~�̒��a�Ŗ��炩��
)�́AAB�͉~�̒��a�Ŗ��炩��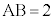 ���A�B�����܂��B
���A�B�����܂��B
����āA�@�C�B���A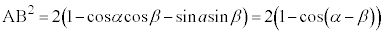
�� 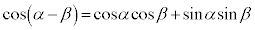 ����C
����C
�C�́A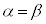 �̂Ƃ����A
�̂Ƃ����A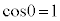 �C
�C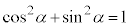 ��萬�����܂��B
��萬�����܂��B
�]���āA�~����ɂǂ̂悤��2�_A�CB���Ƃ��Ă�(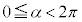 �C
�C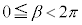 )�A�C�͐������܂��B
)�A�C�͐������܂��B
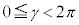 �C
�C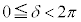 �̂Ƃ��A
�̂Ƃ��A ���������܂����A
���������܂����A
α�Cβ ����ʊp�ł����āAn�Cm�𐮐��Ƃ��āA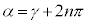 �C
�C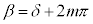 �̂Ƃ��A
�̂Ƃ��A
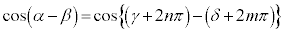
�@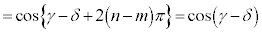
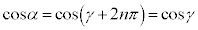
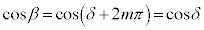
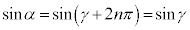
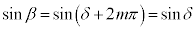 ���A
���A
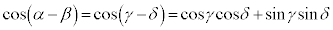
�@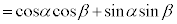
����āA��ʊpα�Cβ �ɂ��Ă��A
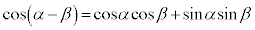 �@����D
�@����D
�D�ɂ����āAβ ��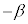 ��������ƁA
��������ƁA
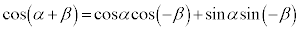
�@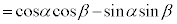 �@����E
�@����E
�E�ɂ����āAα��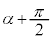 ���������(�O�p���Q��)�A
���������(�O�p���Q��)�A
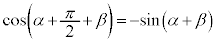
�@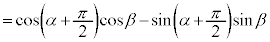
�@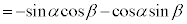
�� 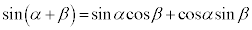 �@����F
�@����F
�F�ɂ����āAβ ��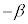 ��������ƁA
��������ƁA
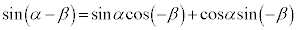
�@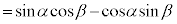
(�ؖ��I)
���@�藝�ɂ��A����Ȋp�̐����E�]���̒l�����߂��܂��B
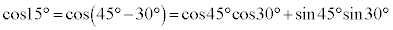
�@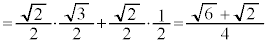
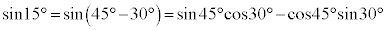
�@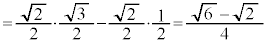
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���w��b����TOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B