�����@�̕������ւ̉��p�@�@�@�֘A���
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
3����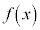 ������Ƃ��ɁA3���������F
������Ƃ��ɁA3���������F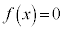 ��3�̑��قȂ���������������́A2��������
��3�̑��قȂ���������������́A2��������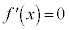 �����قȂ�2�̎�����α�Cβ �������A���A
�����قȂ�2�̎�����α�Cβ �������A���A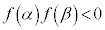 (�ɑ�l�Ƌɏ��l�̐ς���)
(�ɑ�l�Ƌɏ��l�̐ς���)
[�ؖ�]�@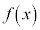 ��
��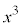 �̌W�������̏ꍇ���l���܂��B���̏ꍇ���S�����l�ł��B�Ȃ��A3�����̑������Q�Ƃ��Ă��������B
�̌W�������̏ꍇ���l���܂��B���̏ꍇ���S�����l�ł��B�Ȃ��A3�����̑������Q�Ƃ��Ă��������B
2��������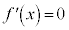 �����قȂ�2�̎�����α�Cβ �����Ƃ��A
�����قȂ�2�̎�����α�Cβ �����Ƃ��A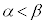 ���Ƃ��āA
���Ƃ��āA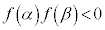 �ł���A�ɑ�l�̕����ɏ��l�����傫���̂ŁA
�ł���A�ɑ�l�̕����ɏ��l�����傫���̂ŁA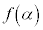 ���ɑ�l��
���ɑ�l��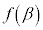 ���ɏ��l�ł���A
���ɏ��l�ł���A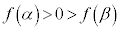 �ł��B
�ł��B
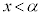 �ɂ����āA
�ɂ����āA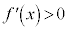 �ł�����
�ł�����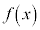 �͒P�������ŁA
�͒P�������ŁA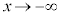 �̂Ƃ�
�̂Ƃ�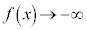 �C�܂��A
�C�܂��A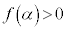 ���A
���A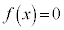 ��
��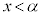 ��1�������������܂��B
��1�������������܂��B
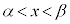 �ɂ����āA
�ɂ����āA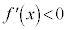 �ł�����
�ł�����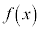 �͒P�������ŁA
�͒P�������ŁA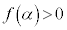 �C
�C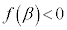 ���A
���A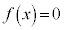 ��
��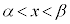 ��1�������������܂��B
��1�������������܂��B
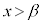 �ɂ����āA
�ɂ����āA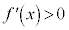 �ł�����
�ł�����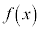 �͒P�������ŁA
�͒P�������ŁA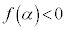 �C
�C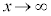 �̂Ƃ�
�̂Ƃ�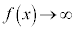 ���A
���A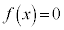 ��
��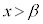 ��1�������������܂��B
��1�������������܂��B
�ȏ���A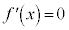 �����قȂ�2�̎�����α�Cβ �������A���A
�����قȂ�2�̎�����α�Cβ �������A���A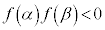 �ł���A3��������
�ł���A3��������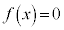 ��3�̑��قȂ�������������܂��B
��3�̑��قȂ�������������܂��B
�܂��A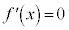 ���d�������ꍇ(���ׂĂ�x�ɂ���
���d�������ꍇ(���ׂĂ�x�ɂ���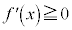 )�A���邢�́A
)�A���邢�́A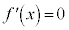 ���������������Ȃ��ꍇ(���ׂĂ�x�ɂ���
���������������Ȃ��ꍇ(���ׂĂ�x�ɂ���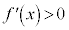 )�́A
)�́A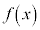 �͒P�������Ȋ��ŁA
�͒P�������Ȋ��ŁA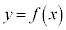 �̃O���t��x���Ƃ���1������_�������܂���B����āA3��������
�̃O���t��x���Ƃ���1������_�������܂���B����āA3��������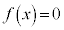 �͂���1�̎��������������܂���B
�͂���1�̎��������������܂���B
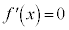 �����قȂ�2�̎�����α�Cβ �����Ƃ��A
�����قȂ�2�̎�����α�Cβ �����Ƃ��A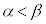 ���Ƃ��āA
���Ƃ��āA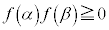 �ł���Ƃ��A
�ł���Ƃ��A
�E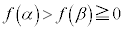 �ł���A3��������
�ł���A3��������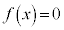 �́A
�́A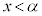 �͈̔͂�1�̎������������܂����A
�͈̔͂�1�̎������������܂����A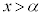 �ɂ�����
�ɂ�����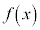 �̍ŏ��l�F
�̍ŏ��l�F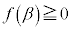 �ł���A
�ł���A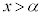 �ɂ����ẮA3��������
�ɂ����ẮA3��������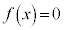 �́A
�́A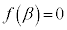 �̂Ƃ��ɁA
�̂Ƃ��ɁA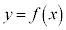 �̃O���t��x���Ɛڂ��A
�̃O���t��x���Ɛڂ��A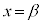 ���d���ɂ����܂����A
���d���ɂ����܂����A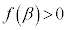 �̂Ƃ��ɂ́A
�̂Ƃ��ɂ́A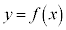 �̃O���t��x���Ƌ��L�_���������������������܂���B
�̃O���t��x���Ƌ��L�_���������������������܂���B
�E �ł���A3��������
�ł���A3��������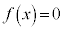 �́A
�́A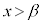 �͈̔͂�1�̎������������܂����A
�͈̔͂�1�̎������������܂����A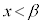 �ɂ�����
�ɂ�����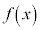 �̍ő�l�F
�̍ő�l�F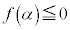 �ł���A
�ł���A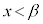 �ɂ����ẮA3��������
�ɂ����ẮA3��������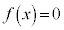 �́A
�́A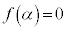 �̂Ƃ�
�̂Ƃ�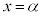 ���d���ɂ����܂����A
���d���ɂ����܂����A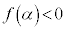 �̂Ƃ��ɂ͎������������܂���B
�̂Ƃ��ɂ͎������������܂���B
�ȏ���A3���������F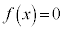 ��3�̑��قȂ���������������́A2��������
��3�̑��قȂ���������������́A2��������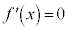 �����قȂ�2�̎�����α�Cβ �������A���A
�����قȂ�2�̎�����α�Cβ �������A���A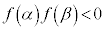 �@(�ؖ��I)
�@(�ؖ��I)
��1�D3���������F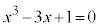 ��3�̈قȂ�������������A���̂�����1��
��3�̈قȂ�������������A���̂�����1��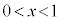 �͈̔͂ɑ��݂��邱�Ƃ������B
�͈̔͂ɑ��݂��邱�Ƃ������B
[��]�@3�����F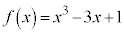 ���l���܂��B
���l���܂��B
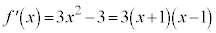
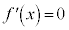 �Ƃ���ƁA
�Ƃ���ƁA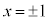
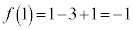
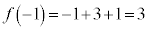
�����\�́A
������A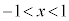 �ɂ�����
�ɂ�����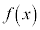 �͒P�������ŁA
�͒P�������ŁA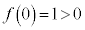 �C
�C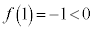 ���A�������F
���A�������F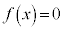 �́A
�́A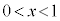 �͈̔͂ɉ��������܂��B
�͈̔͂ɉ��������܂��B
�܂��A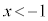 �ɂ�����
�ɂ�����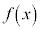 �͒P�������ŁA
�͒P�������ŁA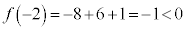 �C
�C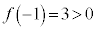 ���A�������F
���A�������F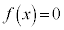 �́A
�́A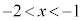 �͈̔͂ɉ��������܂��B
�͈̔͂ɉ��������܂��B
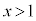 �ɂ�����
�ɂ�����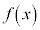 �͒P�������ŁA
�͒P�������ŁA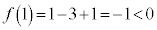 �C
�C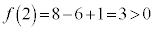 ���A�������F
���A�������F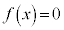 �́A
�́A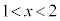 �͈̔͂ɉ��������܂��B
�͈̔͂ɉ��������܂��B
�ȏ���A3���������F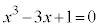 ��3�̈قȂ�������������A���̂�����1��
��3�̈قȂ�������������A���̂�����1��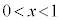 �͈̔͂ɑ��݂��܂��B
�͈̔͂ɑ��݂��܂��B
��2�Dk��萔�Ƃ��āA3���������F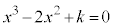 �̉��̌���k�̒l�ɂ��ǂ̂悤�ɕς�邩�ׂ�B
�̉��̌���k�̒l�ɂ��ǂ̂悤�ɕς�邩�ׂ�B
[��]�@3���������F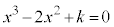 �̉��́A
�̉��́A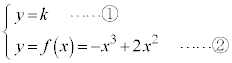 �@��A�������Ƃ��̉��Ɠ����ł��B
�@��A�������Ƃ��̉��Ɠ����ł��B
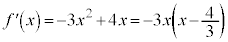
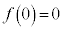
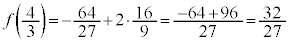
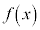 �̑����\�́A
�̑����\�́A
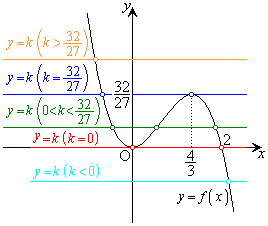 �����\���A
�����\���A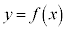 �̃O���t�͉E�}�̂悤�ɂȂ�܂��B
�̃O���t�͉E�}�̂悤�ɂȂ�܂��B
�@�ƇA��A�������Ƃ��̉��́A�@�ƇA�̃O���t�̋��L�_��x���W�ł��B
k�̒l�������Ƃɂ��Ax���ɕ��s�Ȓ����F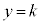 ���㉺�ɓ������Č�_�̐��ׂ�ƁA3���������̉��̌��́A�E�}�̂悤�ɁA
���㉺�ɓ������Č�_�̐��ׂ�ƁA3���������̉��̌��́A�E�}�̂悤�ɁA
1�� (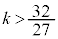 �̂Ƃ�)�C2�� (
�̂Ƃ�)�C2�� (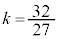 �̂Ƃ�)�C3�� (
�̂Ƃ�)�C3�� (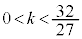 �̂Ƃ�)�C2�� ((
�̂Ƃ�)�C2�� ((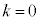 �̂Ƃ�)�C1�� (
�̂Ƃ�)�C1�� (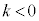 �̂Ƃ�) ......[��]
�̂Ƃ�) ......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���w��b����TOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 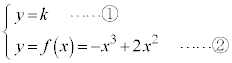 �@��A�������Ƃ��̉��Ɠ����ł��B
�@��A�������Ƃ��̉��Ɠ����ł��B