3次関数の増減 関連問題
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
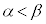 のとき、3次関数:
のとき、3次関数: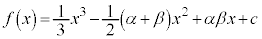 (cは実数の定数)を考える。
(cは実数の定数)を考える。
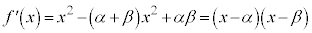 (微分・導関数を参照)
(微分・導関数を参照)
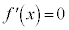 とすると、
とすると、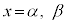
増減表は、
極大値: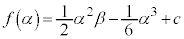 ,極小値:
,極小値: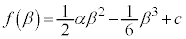
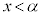 ,
,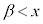 においては、
においては、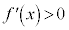 で
で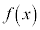 は単調増加 (
は単調増加 (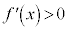 ということは接線の傾きが正で、グラフが右上がりになることを意味する)
ということは接線の傾きが正で、グラフが右上がりになることを意味する)
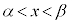 においては、
においては、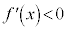 で
で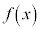 は単調減少 (
は単調減少 (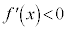 ということは接線の傾きが負で、グラフが右下がりになることを意味する)
ということは接線の傾きが負で、グラフが右下がりになることを意味する)
(このことの証明は、単調増加関数・単調減少関数を参照)
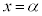 において、
において、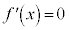 となるが、xが
となるが、xが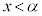 から
から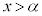 に変化するとき、
に変化するとき、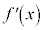 の符号が+から−に変化し、
の符号が+から−に変化し、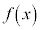 は増加から減少に切り替わる。
は増加から減少に切り替わる。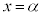 の周辺では
の周辺では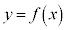 のグラフは
のグラフは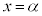 において最大になっている(全実数xでは最大ではない)。このようなとき、
において最大になっている(全実数xでは最大ではない)。このようなとき、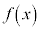 は
は において極大であると言い、
において極大であると言い、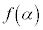 を極大値と言う。
を極大値と言う。
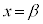 において、
において、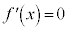 となるが、xが
となるが、xが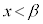 から
から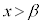 に変化するとき、
に変化するとき、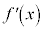 の符号が−から+に変化し、
の符号が−から+に変化し、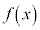 は減少から増加に切り替わる。
は減少から増加に切り替わる。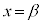 の周辺では
の周辺では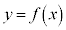 のグラフは
のグラフは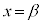 において最小になっている(全実数xでは最小ではない)。このようなとき、
において最小になっている(全実数xでは最小ではない)。このようなとき、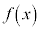 は
は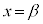 において極小であると言い、
において極小であると言い、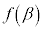 を極小値と言う。
を極小値と言う。
極大値と極小値をまとめて、極値と言う。
注.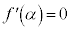 ,
,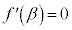 は、
は、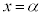 ,
,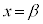 において、
において、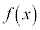 が極大、極小になることの必要条件でも十分条件でもありません(条件・命題を参照)。
が極大、極小になることの必要条件でも十分条件でもありません(条件・命題を参照)。
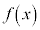 が
が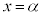 において極大 ⇔ 十分小さなhをとるとき、
において極大 ⇔ 十分小さなhをとるとき、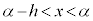 ,
,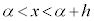 となるすべてのxに対して、
となるすべてのxに対して、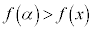
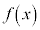 が
が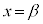 において極小 ⇔ 十分小さなhをとるとき、
において極小 ⇔ 十分小さなhをとるとき、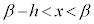 ,
,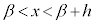 となるすべてのxに対して、
となるすべてのxに対して、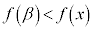
また、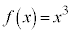 のような関数では、
のような関数では、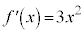 で、
で、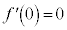 ですが、
ですが、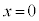 において、
において、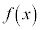 は極大でも極小でもありません。このような場合、
は極大でも極小でもありません。このような場合、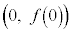 のような点を停留点と言います。
のような点を停留点と言います。
通常の関数では、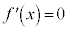 (接線の傾きが0で、接線がx軸に平行になることを意味する)となるときに
(接線の傾きが0で、接線がx軸に平行になることを意味する)となるときに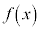 が極値をとることが多いので、
が極値をとることが多いので、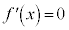 となるところを探します。
となるところを探します。
 例.3次関数:
例.3次関数: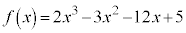 の増減を考えます。
の増減を考えます。
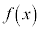 の導関数は、
の導関数は、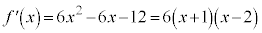
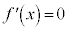 の解は、
の解は、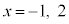
ここで、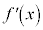 の符号を調べると
の符号を調べると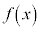 の増減がわかるので、増減表と呼ばれる表を作ります。
の増減がわかるので、増減表と呼ばれる表を作ります。
最上行はxの欄、2行目は導関数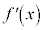 の欄、最下行は
の欄、最下行は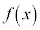 の欄です。
の欄です。
xの欄に、少し間隔をあけて、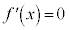 の解を左から小さい順に、ここでは、
の解を左から小さい順に、ここでは、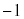 と2を書き込みます。
と2を書き込みます。
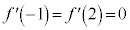 なので、
なので、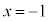 と
と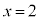 に対応する
に対応する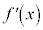 の欄に0を書き込みます。
の欄に0を書き込みます。 の欄には、
の欄には、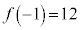 と
と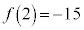 を書き込みます。
を書き込みます。
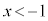 のとき、
のとき、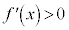 なので、
なので、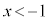 に対応する
に対応する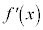 の欄に+を書き込みます。
の欄に+を書き込みます。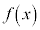 の欄には、
の欄には、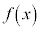 が単調増加で右上がりのグラフになることを示す記号
が単調増加で右上がりのグラフになることを示す記号 を書き込みます。
を書き込みます。
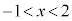 のとき、
のとき、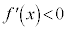 なので、
なので、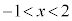 に対応する
に対応する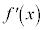 の欄に−を書き込みます。
の欄に−を書き込みます。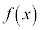 の欄には、
の欄には、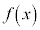 が単調減少で右下がりのグラフになることを示す記号
が単調減少で右下がりのグラフになることを示す記号 を書き込みます。
を書き込みます。
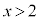 のとき、
のとき、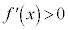 なので、
なので、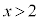 に対応する
に対応する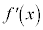 の欄に+を書き込みます。
の欄に+を書き込みます。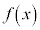 の欄には、
の欄には、 を書き込みます。
を書き込みます。
こうして、以下のような増減表ができます。
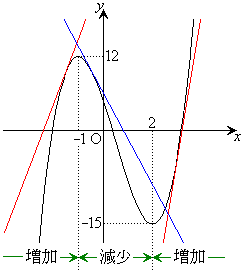
この表だけで、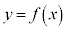 のグラフの概形(右図)が想像できてしまいます。
のグラフの概形(右図)が想像できてしまいます。
また、極大値が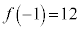 ,極小値が
,極小値が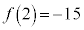 であることもわかります。
であることもわかります。
さて、上記の例においては、3次関数が、極大値と極小値を持ちましたが、3次関数は必ずしも極値をもつとは限りません。
3次関数の増減(2)を参照してください。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
数学基礎事項TOP 数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。