3次関数の増減(2)
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
3次関数の増減の続きです。
3次関数: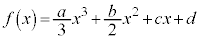 (a,b,c,dは実数の定数で、
(a,b,c,dは実数の定数で、 )を考えます。
)を考えます。
 ですが、
ですが、 は2次方程式:
は2次方程式: ・・・① となります(2次方程式の一般論を参照)。
・・・① となります(2次方程式の一般論を参照)。
①の判別式を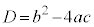 として、以下のように場合分けすることができます。
として、以下のように場合分けすることができます。
 (i)
(i)  のとき、2次方程式:
のとき、2次方程式: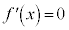 は2個の実数解をもちます。これを、α,β (
は2個の実数解をもちます。これを、α,β (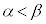 )とすれば、右図のように
)とすれば、右図のように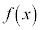 は、
は、
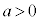 のとき、極大値:
のとき、極大値: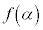 ,極小値:
,極小値: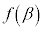 をとります。
をとります。
 のとき、極大値:
のとき、極大値: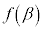 ,極小値:
,極小値: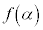 をとります。
をとります。
 (ii)
(ii)  のとき、2次方程式:
のとき、2次方程式: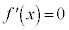 は実数の重解を持ちます。これをαとすれば、
は実数の重解を持ちます。これをαとすれば、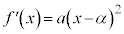 となり、右図のように、
となり、右図のように、
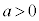 のとき、
のとき、 で、
で、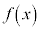 は単調増加(
は単調増加(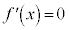 を与えるxが
を与えるxが ただ1つだけの場合にも、
ただ1つだけの場合にも、 の場合と同様に単調増加と言います)であり、
の場合と同様に単調増加と言います)であり、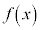 は極値をもちません。
は極値をもちません。
 のとき、
のとき、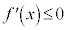 で、
で、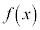 は単調減少であり、
は単調減少であり、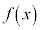 は極値をもちません。
は極値をもちません。
 (iii)
(iii)  のとき、2次方程式:
のとき、2次方程式: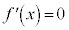 は実数解をもちません。右図のように、
は実数解をもちません。右図のように、
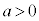 のとき、
のとき、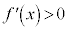 で、
で、 は単調増加であり、
は単調増加であり、 は極値をもちません。
は極値をもちません。
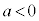 のとき、
のとき、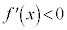 で、
で、 は単調減少であり、
は単調減少であり、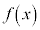 は極値をもちません。
は極値をもちません。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
数学基礎事項TOP 数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。