���̋ߎ��l
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�����\��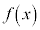 �ɂ��āAa�ɏ\���߂�x�ɂ�������l
�ɂ��āAa�ɏ\���߂�x�ɂ�������l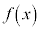 �͈ȉ��̂悤�ɋߎ��ł���B
�͈ȉ��̂悤�ɋߎ��ł���B
(1) 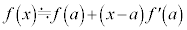
�Ƃ���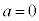 �̏ꍇ�ɂ́A0�ɏ\���߂�x�ɂ�������l
�̏ꍇ�ɂ́A0�ɏ\���߂�x�ɂ�������l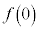 �͈ȉ��̂悤�ɋߎ��ł���B
�͈ȉ��̂悤�ɋߎ��ł���B
(2) 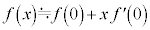
(1)���m���߂Ă����ƁA���ϒl�̒藝���A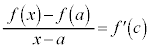 �C
�C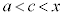 �܂���
�܂���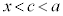
����c�����݂��܂��B����ɂ��A
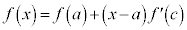 �@����@
�@����@
�܂��A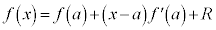 �@����A
�@����A
�Ƃ����ƁA
�@�|�A���A
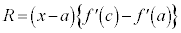
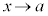 �̂Ƃ��A
�̂Ƃ��A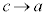 �Ȃ̂ŁA
�Ȃ̂ŁA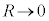
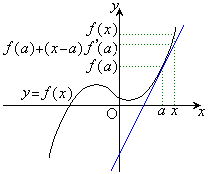 �]���āAa�ɏ\���߂�x�ɂ��ẮA�A����R�����āA
�]���āAa�ɏ\���߂�x�ɂ��ẮA�A����R�����āA
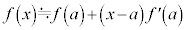
�ƍl���邱�Ƃ��ł��܂��B
����́A�E�}�̂悤�ɁA�Ȑ���̓_��y���W�F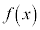 ���A
���A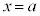 �ɂ�����ڐ��F
�ɂ�����ڐ��F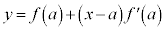 ��̓_��y���W�ő�p���邱�Ƃɑ������܂��B
��̓_��y���W�ő�p���邱�Ƃɑ������܂��B
���̋ߎ����������A����ɐ��x��v�������ꍇ�ɂ́A�e�[���[�W�J�A�}�N���[�����W�J�Ȃǂ̋Z�@��p���܂��B
��1�D��L�̋ߎ�����(1)�ɂ����āA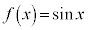 �̏ꍇ�A
�̏ꍇ�A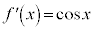 ���A
���A
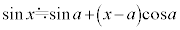
�Ƃ����ߎ�������邱�Ƃ��ł��܂��B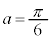 �Ƃ��āA
�Ƃ��āA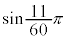 �́A
�́A
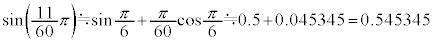
�Ƌߎ��v�Z�ł��܂��B
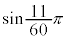 �̐������l�́A
�̐������l�́A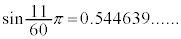 �Ȃ̂ŁA
�Ȃ̂ŁA
���悻3���̐��x�Ő������l�ɂȂ��Ă��܂��B
�e�[���[�W�J�ɂ������F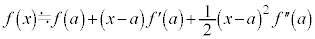 (2���̋ߎ��ƌ����܂�)��p����ƁA
(2���̋ߎ��ƌ����܂�)��p����ƁA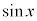 �̋ߎ����́A
�̋ߎ����́A
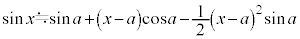
�ƂȂ�A
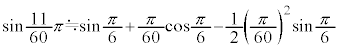
�@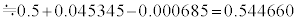
���悻4���̐��x�Ő������l�ɂȂ��Ă��܂��B
��2�D��L�̋ߎ�����(2)�ɂ����āAx�̐�Βl���\���ɏ�������A
(a) 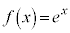 �̏ꍇ�A
�̏ꍇ�A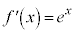 �C
�C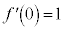 �C
�C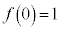 ���A
���A
�@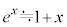
(b) 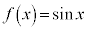 �̏ꍇ�A
�̏ꍇ�A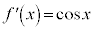 �C
�C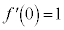 �C
�C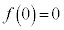 ���A
���A
�@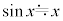
(c) 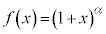 �̏ꍇ�A
�̏ꍇ�A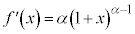 �C
�C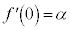 �C
�C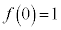 ���A
���A
�@
�Ȃǂ̋ߎ������������܂��B
(c)�ɂ��ƁA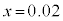 �C
�C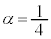 �̏ꍇ�A
�̏ꍇ�A
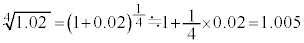
�Ƌߎ��ł��܂��B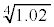 �̐������l�́A
�̐������l�́A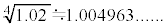 �Ȃ̂ŁA���悻4���̐��x�Ő������l�ɂȂ��Ă��܂��B
�Ȃ̂ŁA���悻4���̐��x�Ő������l�ɂȂ��Ă��܂��B
���̏ꍇ���A��萸�x���グ������A�}�N���[�����W�J�ɂ������F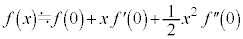 �Ȃǂ�p���邱�ƂɂȂ�܂��B
�Ȃǂ�p���邱�ƂɂȂ�܂��B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���w��b����TOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B