等差数列 関連問題
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
第n項に定数dを加えると第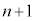
項になる数列を等差数列と言う。定数dを公差と言う。
漸化式：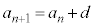
(
)，
(
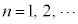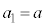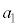：初項)
一般項：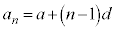
(
)
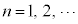第n項までの和：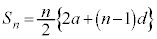
注．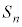
については、
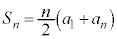((初項＋末項)×項数÷2)という覚え方が便利です。数列の初項は
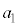とは限りません。入試問題によって、
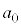とか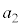
とか、いろいろです。
1, 4, 7, 10, 13, 16, 19, 22, ･･････
のように数が並ぶ数列は、1を初項として、3ずつ増えていく数列です。
このように、決まった数だけ増えていく数列が等差数列です。初項が1，公差は3です。
この数列では、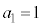
，
，
，
，･･････
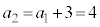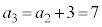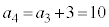のようになっています。
これを一般的に書くと、公差をd，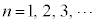
として、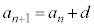
となります(このように、第n項と第n+1項の間の関係を示す式が漸化式です)。
等差数列の一般項(第n項)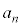
は、初項
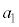に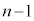
回公差dを加えたものになるので、
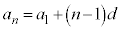となります。
初項を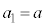
とすれば、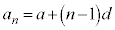
となります。
初項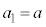
，公差dの等差数列の第n項までの和
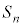は、
(
)
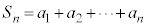
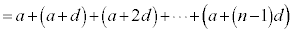
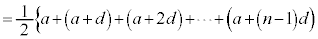
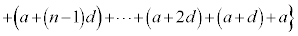
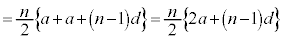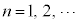3数a，b，cが、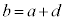
，
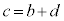のようになっていて、等差数列をなしているとき、
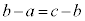より、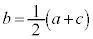
3数のまん中の数は、他の2数の相加平均になっています。このまん中の数bのことを等差中項と言います。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
数学基礎事項TOP 数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中！理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。