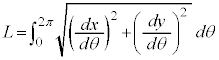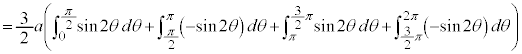アステロイド 関連問題
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
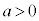 として、媒介変数表示:
として、媒介変数表示: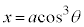 ,
,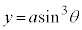 で与えられる曲線をアステロイドと言う。
で与えられる曲線をアステロイドと言う。
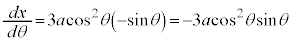 ,
,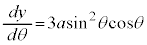 ,
,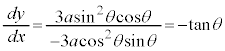 (媒介変数表示された関数の微分法を参照)
(媒介変数表示された関数の微分法を参照)
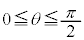 において、
において、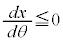 より、xは単調減少,
より、xは単調減少,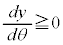 より、yは単調増加で、θ が
より、yは単調増加で、θ が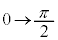 と変わるとき、xは
と変わるとき、xは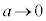 ,yは
,yは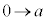 となります。
となります。
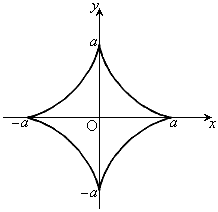 グラフは右図。x軸,y軸に関して対称です。
グラフは右図。x軸,y軸に関して対称です。
右図のアステロイドCが囲む部分の面積Sは、第1象限にある部分を4倍して、
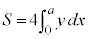
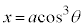 を用いて置換積分を行うと、
を用いて置換積分を行うと、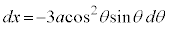 ,x:
,x: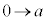 のとき、θ:
のとき、θ: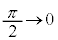 より、
より、
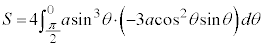
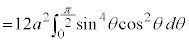
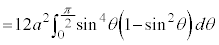
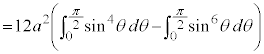
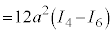 (但し、
(但し、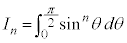 ,定積分の漸化式を参照)
,定積分の漸化式を参照)
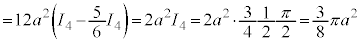
アステロイドCが囲む部分をx軸のまわりに1回転してできる回転体の体積Vは、第1象限にある部分を1回転したものの2倍として、
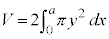
面積と同じように、置換積分を行うと、
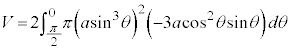
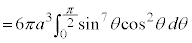
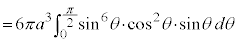
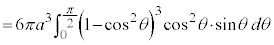
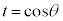 とおく(置換積分を参照)と、
とおく(置換積分を参照)と、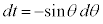 ,θ:
,θ: のとき、t:
のとき、t: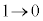 より、
より、
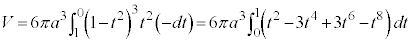
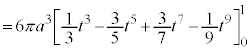
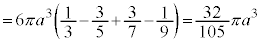
曲線Cの長さLは、第1象限にある部分の長さを4倍して、
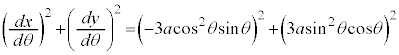
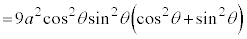
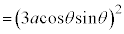
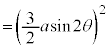
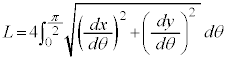
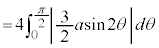
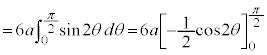
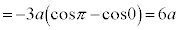
注.この計算を以下のように行うのは誤りです。
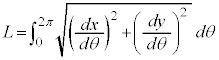
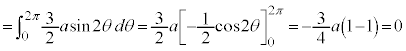 ???
???
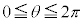 において、つねに
において、つねに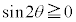 ではないことに注意してください。
ではないことに注意してください。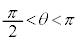 ,
,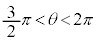 においては、
においては、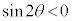 です。
です。
正しくは、以下のようになります(なるべく、解答のように計算してください)。
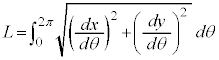
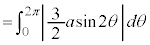
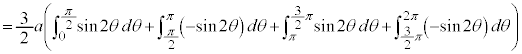
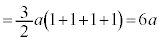
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
数学基礎事項TOP 数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 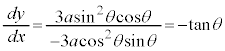 (媒介変数表示された関数の微分法を参照)
(媒介変数表示された関数の微分法を参照)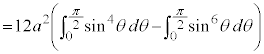
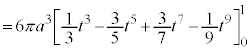
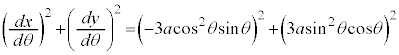
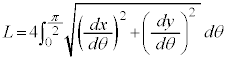
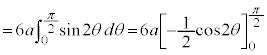
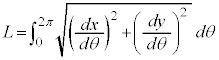
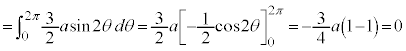 ???
???