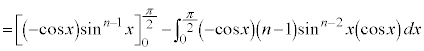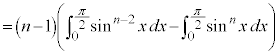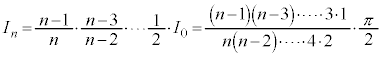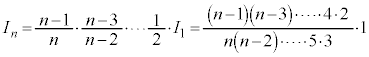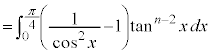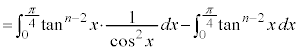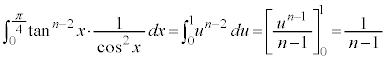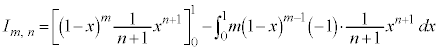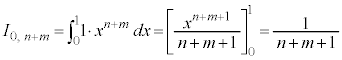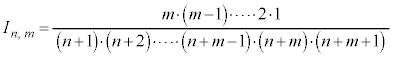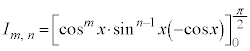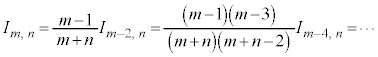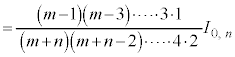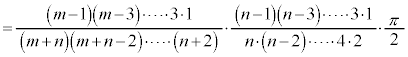定積分の漸化式 関連問題
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
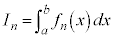と表されるような数列の漸化式を考えます。
積分を数列として捉えることにより、見通しがよくなることがあります。
例1．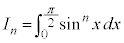 
(
)
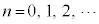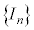の漸化式を作るために、部分積分法で積分します。
∴ 
(
)
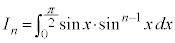
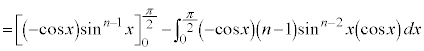
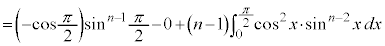
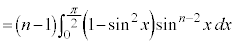
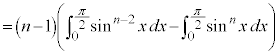
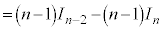
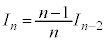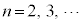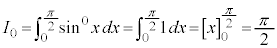
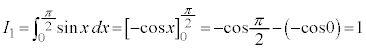
より、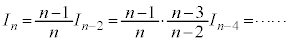
としていくと、
nが偶数のとき、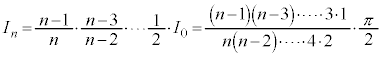
分子に奇数が並び、分母に偶数が並びます。
，
，
，
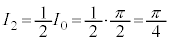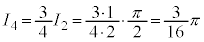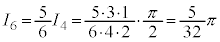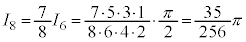
のようになります。
nが奇数のとき、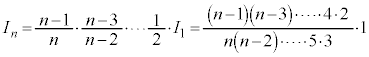
分子に偶数が並び、分母に奇数が並びます。
，
，
，
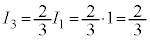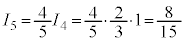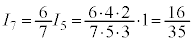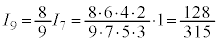
のようになります。
また、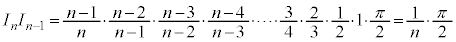
より、
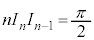
が成り立ちます。
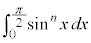という形に積分は入試ではよく見る形なので、上記の
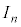の結果は暗記しておくと便利です。
例2．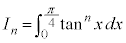 
(
)
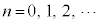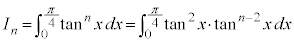
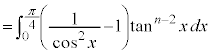
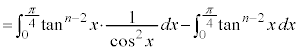
第1項の積分は、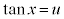
とおく(置換積分を参照)ことにより、
∴ 
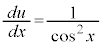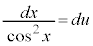
x：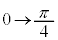
のとき、u：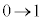
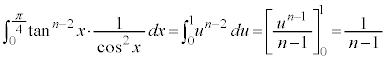
第2項の積分は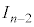
と表せます。
∴ 
(
)
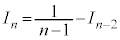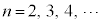例3．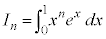 
(
)
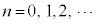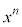を微分、
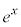を積分に回して、部分積分します。
∴ 
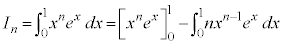
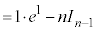
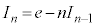
例4．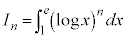 
(
)
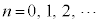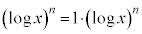とみなして、1を積分、
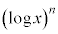を微分に回して、部分積分します。
∴ 
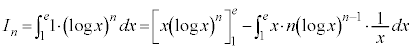
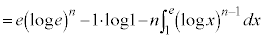
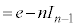
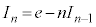
例5．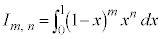 
(
，
)
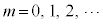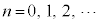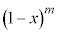を微分、
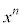を積分に回して、部分積分します。
∴ 
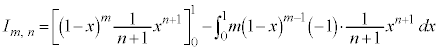
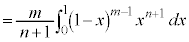
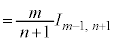
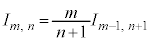
この漸化式をくり返し使うことにより、
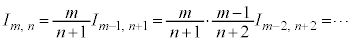
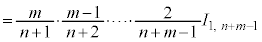(分数の積が出てきますが、各分数で分子と分母の和が
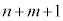になることに注意)
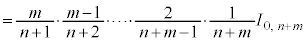
ところで、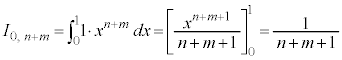
∴ 
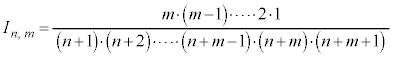
この分子は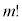
です。分母は、
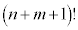を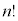
で割ったものになります。従って、
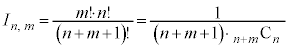(組み合わせを参照)
例6．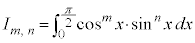 
(
，
)
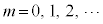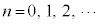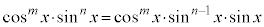と見て、
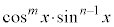を微分、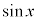
を積分に回して、部分積分します。
∴ 
∴ 
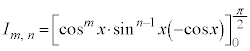
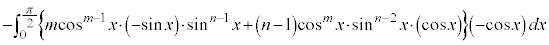
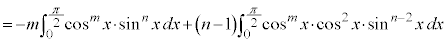
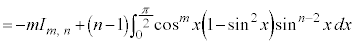
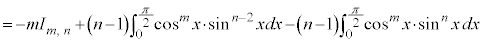
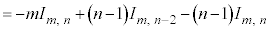
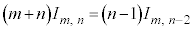
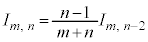
例1．は、これの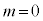
の場合に相当します。
同様に、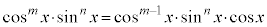
と見て、
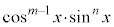を微分、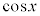
を積分に回して、部分積分すると、
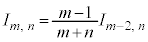
が得られます。
m，nがともに偶数の場合に、これを繰り返して用いると、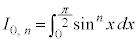
(例1．参照)より、
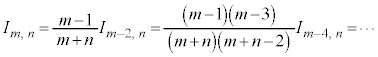
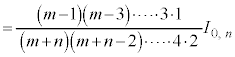
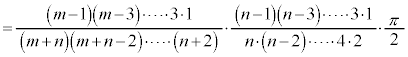
例えば、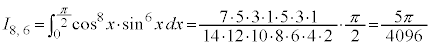
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
数学基礎事項TOP 数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中！理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。