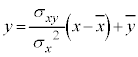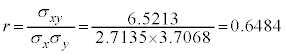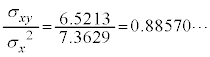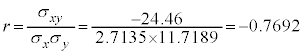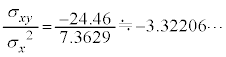相関 関連問題
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
二つの属性について、大きさが同じデータ、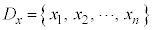 ,
,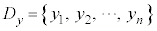 があるとき、座標平面上に
があるとき、座標平面上に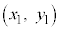 ,
,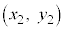 ,・・・,
,・・・,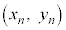 をプロットしたものを散布図と言う。
をプロットしたものを散布図と言う。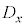 の要素の平均値を
の要素の平均値を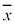 ,
,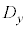 の要素の平均値を
の要素の平均値を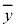 とするとき、
とするとき、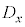 の各要素と
の各要素と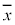 との差(偏差)と
との差(偏差)と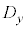 の各要素と
の各要素と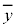 との差(偏差)の積の平均値、
との差(偏差)の積の平均値、
を共分散と言う。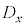 の要素の標準偏差を
の要素の標準偏差を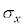 ,
,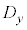 の要素の標準偏差を
の要素の標準偏差を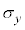 として、
として、
を相関係数と言う。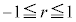 となるが、一般的に以下のことが言える。
となるが、一般的に以下のことが言える。
・rが0に近いとき、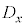 と
と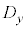 の間には相関がない。
の間には相関がない。 ・rが1に近いとき、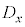 と
と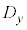 の間には正の相関がある。つまり
の間には正の相関がある。つまり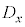 の要素の値が大きくなると
の要素の値が大きくなると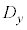 の要素の値も大きくなる。
の要素の値も大きくなる。 ・rが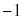 に近いとき、
に近いとき、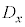 と
と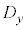 の間には負の相関がある。つまり
の間には負の相関がある。つまり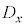 の要素の値が大きくなると
の要素の値が大きくなると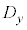 の要素の値は小さくなる。
の要素の値は小さくなる。 直線: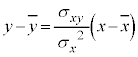 を回帰直線と言う。
を回帰直線と言う。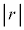 が1に近いときに散布図は回帰直線に近くなる。
が1に近いときに散布図は回帰直線に近くなる。
身長と体重とか、数学の点数と英語の点数とか、2種類の属性について、どんな関係があるのかを調べたいときがあります。そのとき、2種類の属性の相関を考えることになります。相関係数や回帰直線を求めれば、両属性の関係について調べることができます。
共分散についても、分散の公式: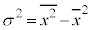 と同様の公式があります。
と同様の公式があります。
よって、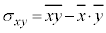
つまり、共分散は、積の平均値から平均値の積を引いたものになります。
相関係数: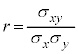 が
が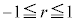 となるのはコーシー・シュワルツの不等式によります。x,yがそれぞれ3通りの値
となるのはコーシー・シュワルツの不等式によります。x,yがそれぞれ3通りの値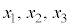 ,
,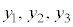 を取るときは、
を取るときは、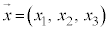 と
と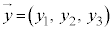 の内積
の内積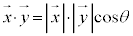 ,
,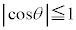 を考えることにより、
を考えることにより、
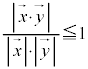 ,即ち、
,即ち、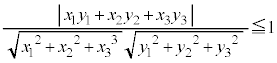
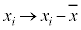 ,
,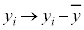 (
(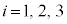 )と見れば、
)と見れば、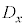 ,
,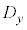 それぞれのデータの大きさが3の場合の
それぞれのデータの大きさが3の場合の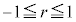 を意味します。n次元ベクトルにおいても、コーシー・シュワルツの不等式:
を意味します。n次元ベクトルにおいても、コーシー・シュワルツの不等式: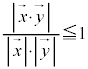 は成立するので、
は成立するので、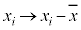 ,
,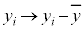 (
(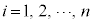 )と見ることにより、一般的な、
)と見ることにより、一般的な、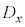 ,
,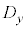 それぞれのデータの大きさがnの場合の相関係数rについても、
それぞれのデータの大きさがnの場合の相関係数rについても、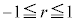 となります。
となります。
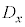 ,
,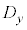 のデータの組
のデータの組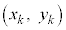 (
(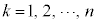 )と、直線
)と、直線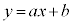 上の点
上の点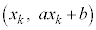 とのy座標の差の2乗の和Sを最小とするa,bを求めてみます。
とのy座標の差の2乗の和Sを最小とするa,bを求めてみます。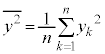 ,
,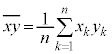 ,
,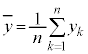 ,
,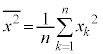 ,
,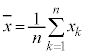 ,
,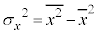 ,
,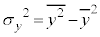 ,
,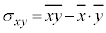 に注意して、
に注意して、
これは、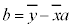 かつ
かつ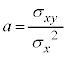 ,つまり、
,つまり、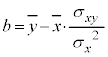 のときに最小になります。従って、散布図を最も良く近似する直線、つまり回帰直線は、
のときに最小になります。従って、散布図を最も良く近似する直線、つまり回帰直線は、
ということになります。傾きが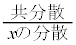 で、平均値を座標とする点
で、平均値を座標とする点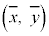 を通る直線です。
を通る直線です。
データの整理で取り上げたデータを再掲します。
| 日 | 最高気温 | 日照時間 | 湿度 | 日 | 最高気温 | 日照時間 | 湿度 | 日 | 最高気温 | 日照時間 | 湿度 |
| 1 | 21.4 | 0 | 71 | 11 | 27.6 | 2.7 | 54 | 21 | 29.3 | 11.4 | 31 |
| 2 | 25.2 | 0.9 | 67 | 12 | 23.5 | 0.9 | 71 | 22 | 31.9 | 6.0 | 46 |
| 3 | 24.7 | 1.4 | 67 | 13 | 26.7 | 7.9 | 37 | 23 | 30.0 | 8.1 | 34 |
| 4 | 24.0 | 0.3 | 71 | 14 | 25.2 | 1.0 | 58 | 24 | 26.2 | 7.9 | 50 |
| 5 | 26.9 | 6.4 | 57 | 15 | 26.3 | 8.6 | 51 | 25 | 27.3 | 8.2 | 46 |
| 6 | 24.9 | 6.5 | 53 | 16 | 27.2 | 5.4 | 45 | 26 | 19.8 | 0.7 | 70 |
| 7 | 26.3 | 9.6 | 44 | 17 | 25.3 | 1.8 | 56 | 27 | 24.9 | 10.5 | 48 |
| 8 | 19.7 | 0 | 68 | 18 | 25.3 | 0 | 71 | 28 | 25.9 | 7.0 | 47 |
| 9 | 28.4 | 6.8 | 55 | 19 | 27.6 | 11.4 | 46 | 29 | 27.7 | 5.7 | 48 |
| 10 | 29.7 | 8.2 | 42 | 20 | 29.0 | 7.8 | 38 | 30 | 27.8 | 7.9 | 48 |
最高気温の平均値は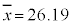 ,分散は、
,分散は、
標準偏差は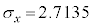 です。
です。
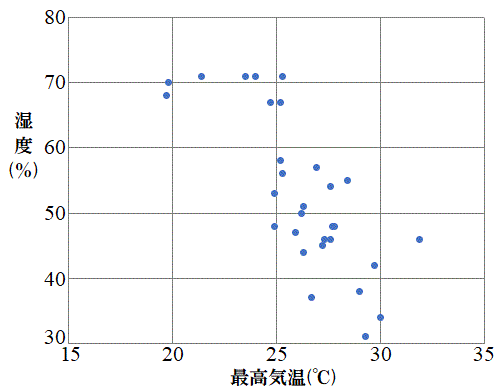
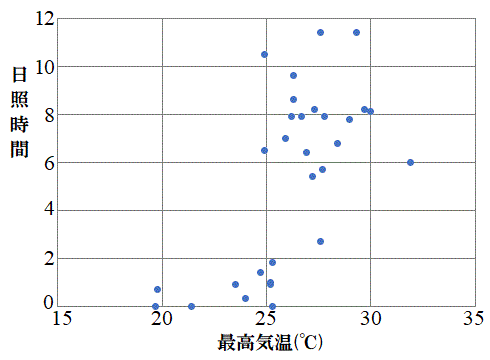 上記のデータについて、最高気温を横軸、日照時間を縦軸に取って作った散布図を右図に示します。
上記のデータについて、最高気温を横軸、日照時間を縦軸に取って作った散布図を右図に示します。
日照時間の平均値は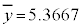 ,分散は、
,分散は、
標準偏差は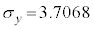 です。
です。
最高気温が高いと日照時間も長くなる傾向があり、正の相関をしていることがわかります。実際に共分散は、
で正です。相関係数は、
で、相関係数も正です。強い相関とまでは言えませんが、かなり強い正の相関です。
より、散布図を近似する直線(回帰直線)は、
です。
 上記のデータについて、最高気温を横軸、湿度を縦軸に取って作った散布図を右図に示します。
上記のデータについて、最高気温を横軸、湿度を縦軸に取って作った散布図を右図に示します。
湿度の平均値は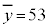 ,分散は、
,分散は、
標準偏差は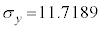 です。
です。
最高気温が高いと湿度は低くなる傾向があり、負の相関をしていることがわかります。実際に共分散は、
で負です。相関係数は、
で、相関係数も負です。強い負の相関です。
より、散布図を近似する直線(回帰直線)は、
です。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
数学基礎事項TOP 数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 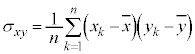
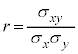
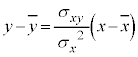 を回帰直線と言う。
を回帰直線と言う。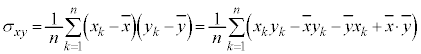
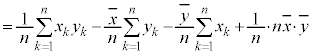
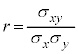 が
が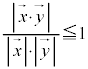 ,即ち、
,即ち、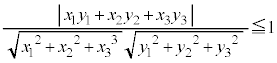
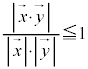 は成立するので、
は成立するので、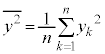 ,
,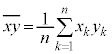 ,
,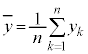 ,
,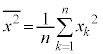 ,
,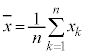 ,
,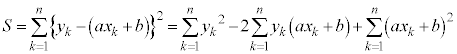
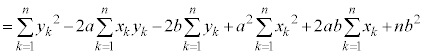
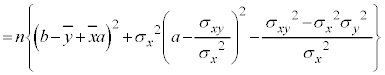
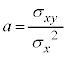 ,つまり、
,つまり、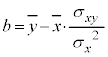 のときに最小になります。従って、散布図を最も良く近似する直線、つまり回帰直線は、
のときに最小になります。従って、散布図を最も良く近似する直線、つまり回帰直線は、