センター数学IA '06年第2問
2次関数
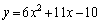･･････①
について考える。
①において、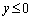
となるxの値の範囲は
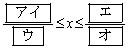
である。
①のグラフをx軸方向にa，y軸方向にbだけ平行移動して得られるグラフをGとする。Gが原点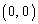
を通るとき、
であり、このときGを表す2次関数は
･･････②
である。
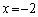と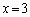
に対応する2次関数②の値が等しくなるのは
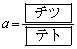
のときである。このとき、2次関数②の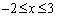
における
最小値は
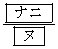，最大値は
である。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
解答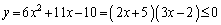 
(2次不等式を参照)
∴ 
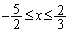
よって、[アイ]は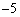
，[ウ]は2，[エ]は2，[オ]は3
①のグラフをx軸方向にa，y軸方向にbだけ平行移動して得られるグラフGを表す2次関数は、
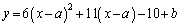･･･③
Gが原点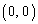
を通るから、
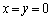を代入して、
∴ 
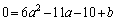
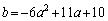･･･④
よって、[カキ]が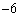
，[クケ]が11，[コサ]が10
このときGを表す2次関数は、④を③に代入して、
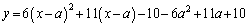
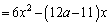･･･⑤
よって、[シ]は6，[スセ]は12，[ソタ]は11
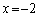と
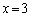に対応する2次関数②の値が等しくなる、ということは、2次関数の軸が、
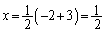にあるという意味で、⑤を平方完成すると、
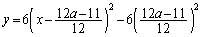･･･⑥
軸の位置：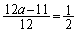
分母を払って、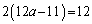
∴ 
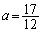･･･⑦
よって、[チツ]は17，[テト]は12
⑦を⑥に代入すると、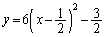
これは、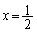
において最小値：
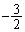をとり、
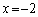と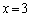
において最大値：
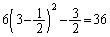(2次関数の最大・最小を参照)
よって、[ナニ]は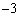
，[ヌ]は2，[ネノ]は36
センター試験の準備は、教科書の基礎事項をしっかりマスターし、ある程度、センター用の練習問題を解いたら、東京出版「センター試験必勝マニュアル 数学IA」(9月頃発売になります)を一通り読んでおきましょう。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中！理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。