センター数学IA '06年第3問
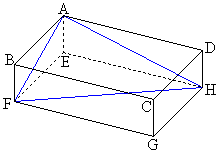 下の図のような直方体ABCD-EFGHにおいて、
下の図のような直方体ABCD-EFGHにおいて、
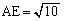 ,
,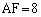 ,
,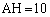
とする。
このとき、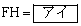 であり、
であり、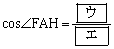 である。
である。
また、三角形AFHの面積は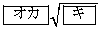 である。
である。
次に、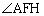 の二等分線と辺AHの交点をP,
の二等分線と辺AHの交点をP,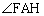 の二等分線と辺FHの交点をQ,線分FPと線分AQの交点をRとする。このとき、Rは三角形AFHの
の二等分線と辺FHの交点をQ,線分FPと線分AQの交点をRとする。このとき、Rは三角形AFHの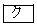 である。次の
である。次の 〜
〜 のうちから
のうちから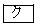 に当てはまるものを一つ選べ。
に当てはまるものを一つ選べ。
 重心
重心  外心
外心  内心
内心
また、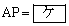 であり、したがって、
であり、したがって、
PF:PR = 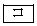 :1
:1
となる。さらに、四面体EAPRの体積は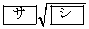 である。
である。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
解答 三平方の定理より、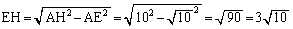 ,
,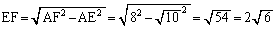 ,
,
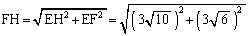
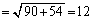
よって、[アイ]は12
余弦定理より、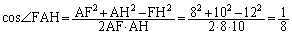
よって、[ウ]は1,[エ]は8
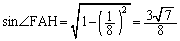
三角形AFHの面積は、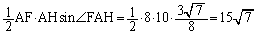
よって、[オカ]は15,[キ]は7
 Rは三角形の各頂角の二等分線の交点で、三角形AFHの内心です。
Rは三角形の各頂角の二等分線の交点で、三角形AFHの内心です。
よって、[ク]は
FPが角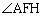 を二等分するので、AF:FH = AP:PH
を二等分するので、AF:FH = AP:PH
∴ 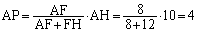
よって、[ケ]は4
ARが角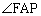 を二等分するので、AF:AP = FR:PR
を二等分するので、AF:AP = FR:PR
これより、PF:PR = 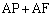 :AP = 3:1
:AP = 3:1
よって、[コ]は3
三角形EAP(右図斜線部)の面積は、三角形AEHの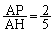 倍で、
倍で、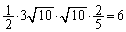
底面を三角形EAPと見るときの四面体EAPRの高さは、ABの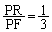 倍で、
倍で、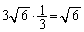
よって、四面体EAPRの体積は、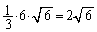
これより、[サ]は2,[シ]は6
センター試験の準備は、教科書の基礎事項をしっかりマスターし、ある程度、センター用の練習問題を解いたら、東京出版「センター試験必勝マニュアル 数学IA」(9月頃発売になります)を一通り読んでおきましょう。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。