センター数学IA '07年第4問
1辺の長さ1の正六角形があり、その頂点の一つをAとする。一つのさいころを3回投げ、点Pを次の(a)，(b)，(c)にしたがって、この正六角形の辺上を反時計回りに進める。
(a) 頂点Aから出発して、1回目に出た目の数の長さだけ点Pを進める。
(b) 1回目で点Pがとまった位置から出発して、2回目に出た目の数の長さだけ点Pを進める。
(c) 2回目で点Pがとまった位置から出発して、3回目に出た目の数の長さだけ点Pを進める。
(1) 3回進めたとき、点Pは正六角形の辺上を1周して、ちょうど頂点Aに到達する目の出方は
通りである。 3回進める間に、点Pが1回も頂点Aにとまらない目の出方は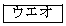
通りである。
(2) 3回進める間に、点Pが3回とも頂点Aにとまる確率は
であり、ちょうど2回だけ頂点Aにとまる確率は
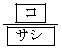である。 3回進める間に、点Pがちょうど1回だけ頂点Aにとまる確率は
である。
(3) 3回進める間に、点Pが頂点Aにとまる回数の期待値は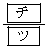
回である。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
解答 (アイ)は数えてしまう方が速いと思います。
(1) 3回で1周して、ちょうどA点に到達するのは、3回の目の和が6になるときで、
(2) さいころを3回振ったときの目の出方は、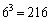
通りあります。 Pが3回ともAに来るのは、3回とも6が出る場合で1通り。その確率は、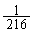
(カ) 1 (キクケ) 216ちょうど2回Aに来るのは、Aに来ないときが1回目なのか、2回目なのか、3回目なのか、3通りあり、その各1通りで、
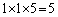通りの目の出方があるので、合わせて、
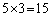通り。
その確率は、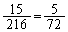
(コ) 5 (サシ) 72 ......[答]ちょうど1回Aに来るのは、Aに来るのが1回目なのか、2回目なのか、3回目なのか、3通りあり、その各1通りで、
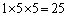通りの目の出方があるので、合わせて、
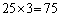通り。
その確率は、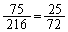
(スセ) 25 (ソタ) 72 ......[答]
(3) PがAに止まる回数の期待値は、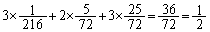
(チ) 1 (ツ) 2 ......[答]
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2023(有)りるらる 苦学楽学塾 随時入会受付中！理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 
，
，
，
，
，
，
，
，
，
の10通り。
通り
通り。