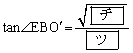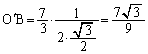センター数学IA '09年第3問
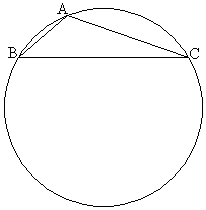△ABCにおいて、
，
，
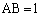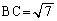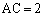とし、
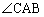の二等分線と辺BCとの交点をDとする。
このとき、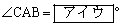
であり
，
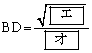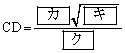
ADの延長と△ABCの外接円Oとの交点のうちAと異なる方をEとする。このとき、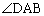
と等しい角は、次の
〜
のうち
と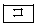
である。ただし、
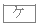と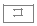
の解答の順序は問わない。
これより、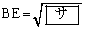
である。また、
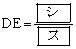である。
次に、△BEDの外接円の中心を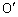
とすると
であり
である。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
解答 センター試験では定番の正弦定理、余弦定理の問題です。
△ABCにおいて余弦定理より、
∴ 
∴ 
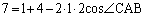
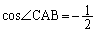
(ア) 1 (イ) 2 (ウ) 0 ......[答]
ADが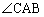
の二等分線であることから、
BD：CD = AB：AC = 1：2
∴ 
，
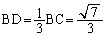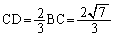
(エ) 7 (オ) 3 (カ) 2 (キ) 7 (ク) 3 ......[答]
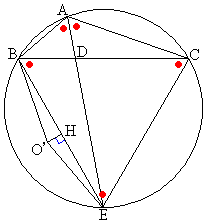ADが
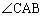の二等分線であることから、
同一弧上に立つ円周角は等しいから、
これより、△BCEは正三角形で、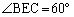
(ケ) (コ) ......[答] (問題文の指示によりケコは逆でもOK)
よって、
(サ) 7 ......[答]
△BDEにおいて余弦定理より、
∴ 
∴ 
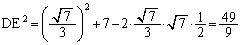
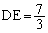
(シ) 7 (ス) 3 ......[答]
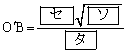
△BEDにおいて正弦定理より、△BEDの外接円の半径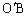
について、
∴ 
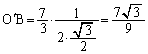
(セ) 7 (ソ) 3 (タ) 9 ......[答]
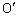よりBEに垂線
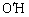を下ろすと、
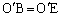よりHはBEの中点で、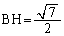
(チ) 3 (ツ) 9 ......[答]
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中！理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。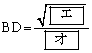 
(
)
