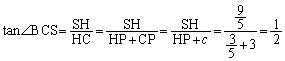�@�Z���^�[���wIA '10�N��3��@
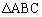 ��
��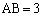 �C
�C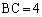 �C
�C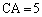 �ł��钼�p�O�p�`�Ƃ���B
�ł��钼�p�O�p�`�Ƃ���B
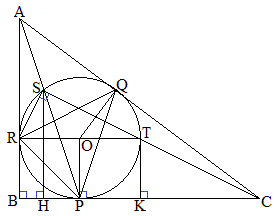
(1) 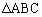 �̓��ډ~�̒��S��O�Ƃ��A�~O��3��BC�CCA�CAB�Ɛڂ���_�����ꂼ��P�CQ�CR�Ƃ���B���̂Ƃ��A
�̓��ډ~�̒��S��O�Ƃ��A�~O��3��BC�CCA�CAB�Ɛڂ���_�����ꂼ��P�CQ�CR�Ƃ���B���̂Ƃ��A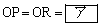 �ł���B�܂��A
�ł���B�܂��A 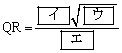 �ł���A
�ł���A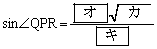 �ł���B
�ł���B(2) �~O�Ɛ���AP�Ƃ̌�_�̂���P�ƈقȂ����S�Ƃ���B���̂Ƃ��A
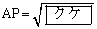 �ł���A
�ł���A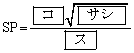 �ł���B�܂��A�_S�����BC���������낵�A������BC�Ƃ̌�_��H�Ƃ���B���̂Ƃ�
�ł���B�܂��A�_S�����BC���������낵�A������BC�Ƃ̌�_��H�Ƃ���B���̂Ƃ�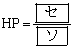 �C
�C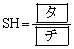
�ł���B���������āA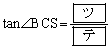 �ł���B
�ł���B (3) �~O��ɓ_T�����RT���~O�̒��a�ƂȂ�悤�ɂƂ�B���̂Ƃ��A
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@���ׂ��̒藝���g���Ƃ��낪�|�C���g�ł��B���ׂ��̒藝���v�����Ȃ���A�O�p�`ASR�ƎO�p�`ARP�̑������l���܂��B
�@�{�A�{�B���A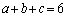 �@����C
�@����C
�C�|�A���A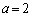
�C�|�B���A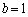
�C�|�@���A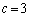
�l�p�`BPOR�͐����`�Ȃ̂ŁA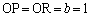 (�A) 1 ......[��]�]���āA�O�p�`ABC�̓��ډ~O�̔��a��1�ł��B
(�A) 1 ......[��]�]���āA�O�p�`ABC�̓��ډ~O�̔��a��1�ł��B
�O�p�`AQR���]���藝��K�p���āA �� 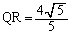
(�C) 4�@(�E) 5�@(�G) 5 ......[��]�O�p�`PQR�̊O�ډ~�̔��a��1�Ȃ̂ŁA�O�p�`PQR�������藝��K�p���āA (�I) 2�@(�J) 5�@(�L) 5 ......[��]
(2) ���p�O�p�`ABP�ɂ����āA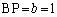 �ƎO�����̒藝���A
�ƎO�����̒藝���A �� 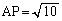
(�N) 1�@(�P) 0 ......[��]����AP�͉~O��2�_P�CS�Ō����A����AB�͉~O��R�Őڂ���̂ŁA���ׂ��̒藝���A �� 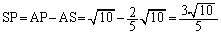
(�R) 3�@(�T) 1�@(�V) 0�@(�X) 5 ......[��]
SH // AB���A AP�FSP = BP�FHP = AB�FSH =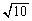 �F
�F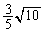 = 5�F3
= 5�F3 �� 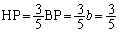 ��
�� 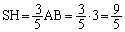
(�Z) 3�@(�\) 5�@(�^) 9�@(�`) 5�@(�c) 1�@(�e) 2 ......[��]
(3) T�����BC�ɐ���TK�����낷�ƁA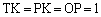
(�g) 1�@(�i) 2 ......[��]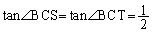 ���A3�_C�CT�CS�͈꒼����ɂ���܂��BRT�͉~O�̒��a��
���A3�_C�CT�CS�͈꒼����ɂ���܂��BRT�͉~O�̒��a��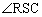 �͒��a�̏�ɗ��~���p�ŁA
�͒��a�̏�ɗ��~���p�ŁA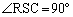
�܂��A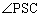 �͉~O�̌�PT�̏�ɗ��~���p�ŁA���S�p
�͉~O�̌�PT�̏�ɗ��~���p�ŁA���S�p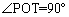 ��
��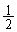
�� 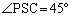
(�j) 9�@(�k) 0�@(�l) 4�@(�m) 5 ......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B  �ł���A
�ł���A �ł���B�܂��A�_S�����BC���������낵�A������BC�Ƃ̌�_��H�Ƃ���B���̂Ƃ�
�ł���B�܂��A�_S�����BC���������낵�A������BC�Ƃ̌�_��H�Ƃ���B���̂Ƃ�