センター数学IA '13年第2問
座標平面上にある点Pは、点A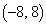 から出発して、直線
から出発して、直線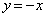 上をx座標が1秒あたり2増加するように一定の速さで動く。また、同じ座標平面上にある点Qは、点PがAを出発すると同時に原点Oから出発して、直線
上をx座標が1秒あたり2増加するように一定の速さで動く。また、同じ座標平面上にある点Qは、点PがAを出発すると同時に原点Oから出発して、直線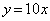 上をx座標が1秒あたり1増加するように一定の速さで動く。出発してからt秒後の2点P,Qを考える。点PがOに達するのは
上をx座標が1秒あたり1増加するように一定の速さで動く。出発してからt秒後の2点P,Qを考える。点PがOに達するのは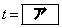 のときである。以下、
のときである。以下、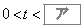 で考える。
で考える。 (1) 点Pとx座標が等しいx軸上の点を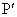 ,点Qとx座標が等しいx軸上の点を
,点Qとx座標が等しいx軸上の点を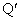 とおく。
とおく。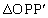 と
と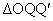 の面積の和Sをt で表せば
の面積の和Sをt で表せば となる。これより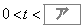 においては、
においては、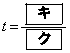 でSは最小値
でSは最小値 をとる。
をとる。
次に、aを を満たす定数とする。以下、
を満たす定数とする。以下、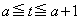 におけるSの最小・最大について考える。
におけるSの最小・最大について考える。 (i) Sが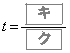 で最小となるようなaの値の範囲は
で最小となるようなaの値の範囲は 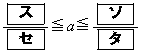 である。
である。(ii) Sが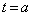 で最大となるようなaの値の範囲は
で最大となるようなaの値の範囲は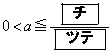 である。
である。 (2) 3点O,P,Qを通る2次関数のグラフが関数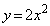 のグラフを平行移動したものになるのは、
のグラフを平行移動したものになるのは、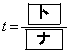 のときであり、x軸方向に
のときであり、x軸方向に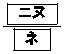 ,y軸方向に
,y軸方向に だけ平行移動すればよい。
だけ平行移動すればよい。 解答 動点を扱うところが珍しいですが、例年通りの2次方程式、2次関数の問題です。
点Pのt 秒後のx座標は、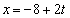
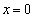 となるのは、
となるのは、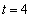 のときです。
のときです。
(ア) 4 ......[答]
(1) 点Pのy座標は、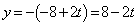
(イ) 7 (ウ) 1 (エ) 6 (オ) 3 (カ) 2 ......[答]
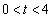 において、Sは、
において、Sは、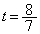 のとき、最小値
のとき、最小値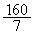 をとります(2次関数の最大最小を参照)。(キ) 8 (ク) 7 (ケ) 1 (コ) 6 (サ) 0 (シ) 7 ......[答]
をとります(2次関数の最大最小を参照)。(キ) 8 (ク) 7 (ケ) 1 (コ) 6 (サ) 0 (シ) 7 ......[答]
Sが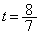 で最小になるのは、
で最小になるのは、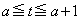 の範囲が
の範囲が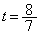 を含むときで、
を含むときで、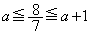 となるとき、つまり、
となるとき、つまり、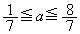 のときです。(ス) 1 (セ) 7 (ソ) 8 (タ) 7 ......[答]
のときです。(ス) 1 (セ) 7 (ソ) 8 (タ) 7 ......[答]
Sをt の関数として表したグラフは放物線で、軸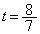 に関して対称なので、
に関して対称なので、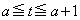 の範囲のちょうど中間に
の範囲のちょうど中間に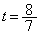 が来るとき、つまり、
が来るとき、つまり、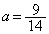 のときに、範囲の両端
のときに、範囲の両端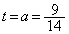 と
と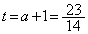 とでSの値が等しくなります。
とでSの値が等しくなります。
従って、Sが左端の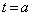 で最大となるのは、
で最大となるのは、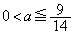 のときです。(チ) 9 (ツ) 1 (テ) 4 ......[答]
のときです。(チ) 9 (ツ) 1 (テ) 4 ......[答]
(2) 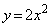 のグラフをx方向にp,y方向にq平行移動したグラフの曲線を
のグラフをx方向にp,y方向にq平行移動したグラフの曲線を とすると、Oを通ることから、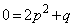 ∴
∴ 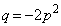 ・・・①P
・・・①P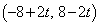 を通ることから、
を通ることから、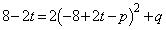 ・・・②Q
・・・②Q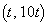 を通ることから、
を通ることから、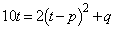 ・・・③
・・・③
①,③より、 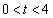 より、
より、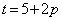 ・・・③
・・・③
これと、①,②より、∴ 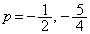 ③より
③より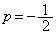 のときには、
のときには、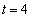 となり不適。よって、
となり不適。よって、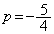 ,
,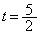
このとき、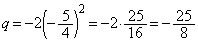 (ト) 5 (ナ) 2 (ニ) - (ヌ) 5 (ネ) 4 (ノ) - (ハ) 2 (ヒ) 5 (フ) 8 ......[答]
(ト) 5 (ナ) 2 (ニ) - (ヌ) 5 (ネ) 4 (ノ) - (ハ) 2 (ヒ) 5 (フ) 8 ......[答]
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。  でSは最小値
でSは最小値 をとる。
をとる。 で最小となるようなaの値の範囲は
で最小となるようなaの値の範囲は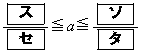 である。
である。 である。
である。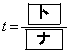 のときであり、x軸方向に
のときであり、x軸方向に ,y軸方向に
,y軸方向に だけ平行移動すればよい。
だけ平行移動すればよい。