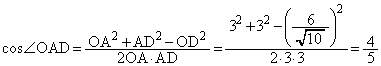センター数学IA '13年第3問
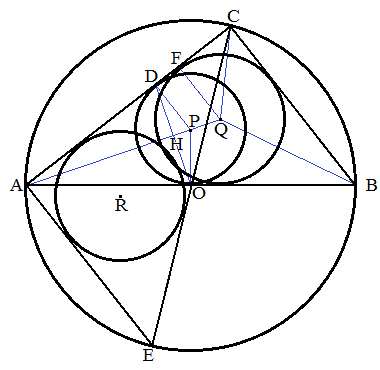
点Oを中心とする半径3の円Oと、点Oを通り、点Pを中心とする半径1の円Pを考える。円Pの点Oにおける接線と円Oとの交点をA,Bとする。また、円Oの周上に、点Bと異なる点Cを、弦ACが円Pに接するようにとる。弦ACと円Pの接点をDとする。このとき
 ,
,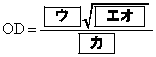
である。さらに、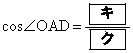 であり、
であり、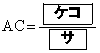 である。
である。
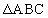 の面積は
の面積は であり、
であり、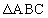 の内接円の半径は
の内接円の半径は である。
である。(1) 円Oの周上に、点Eを線分CEが円Oの直径となるようにとる。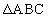 の内接円の中心をQとし、
の内接円の中心をQとし、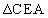 の内接円の中心をRとする。このとき、
の内接円の中心をRとする。このとき、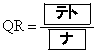 である。したがって、内接円Qと内接円Rは
である。したがって、内接円Qと内接円Rは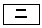 。
。  に当てはまるものを、次の
に当てはまるものを、次の 〜
〜 のうちから一つ選べ。
のうちから一つ選べ。
 内接する
内接する  異なる2点で交わる
異なる2点で交わる
 外接する
外接する  共有点を持たない
共有点を持たない(2) 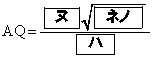 であるから、
であるから、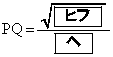 となる。
となる。 したがって、 。
。
 に当てはまるものを、次の
に当てはまるものを、次の 〜
〜 のうちから一つ選べ。
のうちから一つ選べ。
 点Pは内接円Qの周上にある
点Pは内接円Qの周上にある
 点Qは円Pの周上にある
点Qは円Pの周上にある
 点Pは内接円Qの内部にあり、点Qは円Pの内部にある
点Pは内接円Qの内部にあり、点Qは円Pの内部にある
 点Pは内接円Qの内部にあり、点Qは円Pの外部にある
点Pは内接円Qの内部にあり、点Qは円Pの外部にある
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
解答 図が描きにくい問題で、ODの長さで行き詰まった受験生が多かったようですが、直角三角形の相似に気づけば大したことはありません。
後半では、昨年に引き続き、2円の位置関係が問われています。
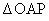 は直角三角形です。三平方の定理より、
は直角三角形です。三平方の定理より、
(ア) 1 (イ) 0 ......[答]
APは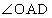 の2等分線なので、
の2等分線なので、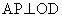
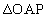 ∽
∽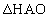 より、AP:OP = AO:OH
より、AP:OP = AO:OH
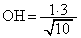 ,
,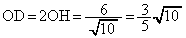
余弦定理より、
(キ) 4 (ク) 5 ......[答]
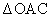 において余弦定理より、
において余弦定理より、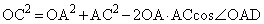
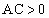 より、
より、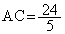
(ケ) 2 (コ) 4 (サ) 5 ......[答]
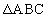 の面積は、
の面積は、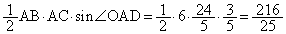 (三角形の面積を参照)
(三角形の面積を参照)
(シ) 2 (ス) 1 (セ) 6 (ソ) 2 (タ) 5 ......[答]
内接円の半径をrとして、
∴ 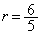 ......[答]
......[答]
(チ) 6 (ツ) 5 ......[答]
(1) 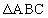 ,
,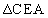 において、
において、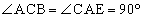 ,
,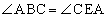 (円周角),AC共通より、
(円周角),AC共通より、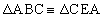
従って、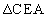 の内接円の半径も
の内接円の半径も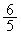 です。また、QR // ACであって、
です。また、QR // ACであって、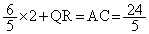 ∴
∴ 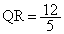
(テ) 1 (ト) 2 (ナ) 5 ......[答]よって、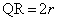 より、内接円Qと内接円Rは外接します。(ニ)
より、内接円Qと内接円Rは外接します。(ニ)  ......[答]
......[答]
(2) 円QとACとの接点をFとすると、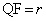 ,
,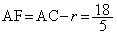
(ヌ) 6 (ネ) 1 (ノ) 0 (ハ) 5 ......[答]円P,円Qともに、AB,ACに接するので、A,P,Qは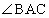 の2等分線上の点です。
の2等分線上の点です。 (ヒ) 1 (フ) 0 (ヘ) 5 ......[答]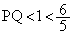 より、点Pは内接円Qの内側の点であって、点Qは円Pの内側の点です。(ホ)
より、点Pは内接円Qの内側の点であって、点Qは円Pの内側の点です。(ホ)  ......[答]
......[答]
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 
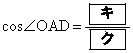 であり、
であり、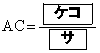 である。
である。 であり、
であり、 である。
である。
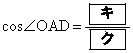 であり、
であり、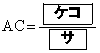 である。
である。 であり、
であり、 である。
である。 である。したがって、内接円Qと内接円Rは
である。したがって、内接円Qと内接円Rは であるから、
であるから、 となる。
となる。