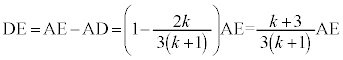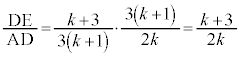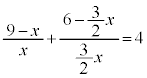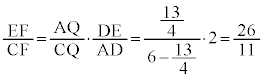�@���ʃe�X�g���wIA '22�N��5��@
��ABC�̏d�S��G�Ƃ��A����AG��œ_A�Ƃ͈قȂ�ʒu�ɓ_D���Ƃ�B����AG�ƕ�BC�̌�_��E�Ƃ���B�܂��A����BC��ŕ�BC��ɂ͂Ȃ��ʒu�ɓ_F���Ƃ�B����DF�ƕ�AB�̌�_��P�C����DF�ƕ�AC�̌�_��Q�Ƃ���B
(1)�@�_D�͐���AG�̒��_�ł���Ƃ���B���̂Ƃ��A��ABC�̌`��ɊW�Ȃ�
�ł���B�܂��A�_F�̈ʒu�ɊW�Ȃ�
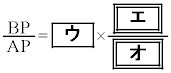 �C
�C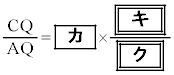
�ł���̂ŁA�˂�
�ƂȂ�B
 �C
�C �C
�C �C
�C �̉Q(�������̂��J��Ԃ��I��ł��悢�B)
�̉Q(�������̂��J��Ԃ��I��ł��悢�B) �@BC�@�@
�@BC�@�@ �@BF�@�@
�@BF�@�@ �@CF�@�@
�@CF�@�@ �@EF
�@EF �@FP�@�@
�@FP�@�@ �@FQ�@�@
�@FQ�@�@ �@PQ
�@PQ
(2)�@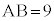 �C
�C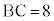 �C
�C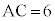 �Ƃ��A(1)�Ɠ��l�ɁA�_D�͐���AG�̒��_�ł���Ƃ���B�����ŁA4�_B�CC�CQ�CP������~����ɂ���悤�ɓ_F���Ƃ�B
�Ƃ��A(1)�Ɠ��l�ɁA�_D�͐���AG�̒��_�ł���Ƃ���B�����ŁA4�_B�CC�CQ�CP������~����ɂ���悤�ɓ_F���Ƃ�B ���̂Ƃ��A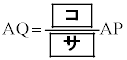 �ł��邩��
�ł��邩�� 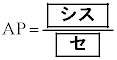 �C
�C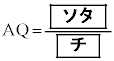
�ł���
�ł���B
(3)�@��ABC�̌`���_F�̈ʒu�ɊW�Ȃ��A�Ȃ�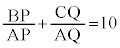 �ƂȂ�̂́A
�ƂȂ�̂́A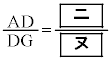 �̂Ƃ��ł���B
�̂Ƃ��ł���B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@���l���E�X�̒藝�ƕ��ׂ��̒藝���g�������Ȃ̂ŁA��3��`��5��̑I����̒��ł͍ł������Ղ����ł��B
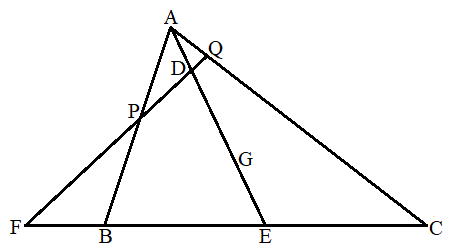 (1)�@AG�FGE = 2�F1�CAD�FDG = 1�F1�Ȃ̂ŁA
(1)�@AG�FGE = 2�F1�CAD�FDG = 1�F1�Ȃ̂ŁA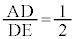
�A�@1�@�C�@2 ......[��]���������́A(3)���l�����A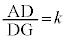 �Ƃ����čl���܂��B(1)�ł́A
�Ƃ����čl���܂��B(1)�ł́A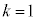 �ł��B
�ł��B 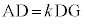 �C
�C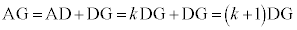
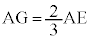 ���A
���A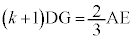
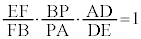 �@��
�@�� 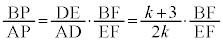 �@����@
�@����@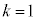 �܂�
�܂�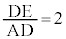 �̂Ƃ��ɂ́A
�̂Ƃ��ɂ́A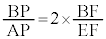
�E�@2�@�G�@1�@�I�@3 ......[��]
CQ�CQA�CAD�CDE���o�Ă���悤�Ƀ��l���E�X�̒藝���g���܂��B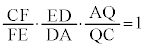 �@��
�@�� 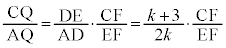 �@����A
�@����A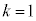 �܂�
�܂�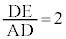 �̂Ƃ��ɂ́A
�̂Ƃ��ɂ́A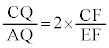
�J�@2�@�L�@2�@�N�@3 ......[��]�@�C�A���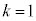 �Ȃ̂ŁA
�Ȃ̂ŁA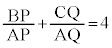 �@����C
�@����C�R�@3�@�T�@2 ......[��]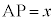 �Ƃ����ƁA
�Ƃ����ƁA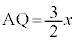 �C
�C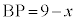 �C
�C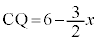
�����ł�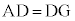 �Ȃ̂�
�Ȃ̂�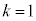 �C����ćC���A
�C����ćC���A �V�X�@13�@�Z�@6�@�\�^�@13�@�`�@4 ......[��]
(1)�Ɠ��l�ɂ����ł�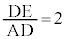 �Ȃ̂ŁA���l���E�X�̒藝���A
�Ȃ̂ŁA���l���E�X�̒藝���A �c�e�@44�@�g�i�@15 ......[��]
(3)�@�B���A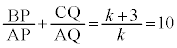
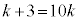 �@��
�@�� 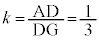
�j�@1�@�k�@3 ......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 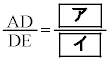
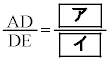
 �C
�C
 �ł��邩��
�ł��邩�� �C
�C
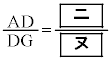 �̂Ƃ��ł���B
�̂Ƃ��ł���B