共通テスト数学IA '23年第3問
番号によって区別された複数の球が、何本かのひもでつながれている。ただし、各ひもはその両端で二つの球をつなぐものとする。次の条件を満たす球の塗り分け方(以下、球の塗り方)を考える。
−条件−−−−−−−−−−−−−
・それぞれの球を、用意した5色(赤、青、黄、緑、紫)のうちのいずれか1色で塗る。
・1本のひもでつながれた二つの球は異なる色になるようにする。
・同じ色を何回使ってもよく、また使わない色があってもよい。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
解答 「構想」のヒントがついていて例年と比較して軽い感じがしますが、基礎学力を見る共通テストとしては、この程度の難度が適切だと思います。なお、場合の数を参照してください。
(1) 球1の塗り方が5通りあり、球2の塗り方が球1で使った色以外の4通りあり、球3の塗り方が球2で使った色以外の4通りあり、球4の塗り方が球3で使った色以外の4通りあります。球の塗り方の総数は、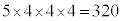
通り。 アイウ 320 ......[答]
(2) 球1の塗り方が5通りあり、球2の塗り方が球1で使った色以外の4通りあり、球3の塗り方が、球1で使った色、球2で使った色以外の3通りあります。球の塗り方の総数は、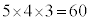
通り。 エオ 60 ......[答]
(3) 球1と球3が赤になるか、球2と球4が赤になるか、です。球1と球3が赤になる場合、球2の塗り方が赤以外の4通り、球4の塗り方が赤以外の4通りで、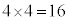
通りの塗り方があります。球2と球4が赤になる場合も16通り。球の塗り方の総数は、
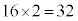通り。 カキ 32 ......[答]
(4) 球1が赤ということはありません。球2〜球6の中にも赤があるからです。同様に、球1が青ということもありません。球1の塗り方は、赤、青以外の3通りです。赤3回、青2回なので、球2〜球6は5球のうちどの2球を青(残りの3球は赤)にするかと考え、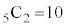
通り(組み合わせを参照)。球の塗り方の総数は、
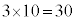通り。 クケ 30 ......[答]
(5) 図Fにおいて、球3と球4が同色でこの塗り方が5通り、球1の塗り方が球3で使った色以外の4通り、球2の塗り方が、球3で使った色、球1で使った色以外の3通りあり、色の塗り方の総数は、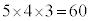
通りです。これと同じ状況になるのは、(2)の場合の
です。 コ 2 ......[答] 図Dにおける球の塗り方の総数は、(1)の結果から60を引いて、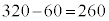
通り。 サシス 260 ......[答]
(6) (5)と同様に考えます。球1と球5の間のひもを取ると、(1)と同様に考えて、球の塗り方は、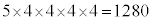
通り。(5)と同様に、球1と球5を同一球として考えると(5)の図Dの状況となり(5)の結果より、球の塗り方は260通り。球の塗り方の総数は、
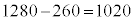通り。 セソタチ 1020 ......[答]
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中！理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 
例えば図Aでは、三つの球が2本のひもでつながれている。この三つの球を塗るとき、球1の塗り方が5通りあり、球1を塗った後、球2の塗り方は4通りあり、さらに球3の塗り方は4通りある。したがって、球の塗り方の総数は80である。
(1) 図Bにおいて、球の塗り方は
通りある。
(2) 図Cにおいて、球の塗り方は
通りある。
(3) 図Dにおける球の塗り方のうち、赤をちょうど2回使う塗り方は
通りある。
(4) 図Eにおける球の塗り方のうち、赤をちょうど3回使い、かつ青をちょうど2回使う塗り方は
通りある。
(5) 図Dにおいて、球の塗り方の総数を求める。そのために、次の構想を立てる。
図Dと図Fを比較する。
図Fにおける球の塗り方は、図Bにおける球の塗り方と同じであるため、全部で
通りある。そのうち球3と球4が同色になる球の塗り方の総数と一致する図として、右の
〜
のうち、正しいものは
である。したがって、図Dにおける球の塗り方は
通りある。
(6) 図Gにおいて、球の塗り方は
通りある。