�@���ʃe�X�g���wIA '23�N��4��@
�F�̂��������`����ׂĐ����`�Ⓑ���`����邱�Ƃ��l����B�F�̂��������`�́A������ς����ɂ����ԂȂ����ׂ邱�ƂƂ��A�F�̂��������`�͏\��������̂Ƃ���B
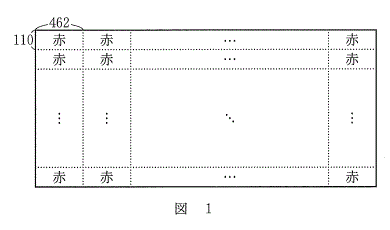 (1)�@���̒�����462�ŏc�̒�����110�ł���Ԃ������`���A�}1�̂悤�ɕ��ׂĐ����`�Ⓑ���`����邱�Ƃ��l����B
(1)�@���̒�����462�ŏc�̒�����110�ł���Ԃ������`���A�}1�̂悤�ɕ��ׂĐ����`�Ⓑ���`����邱�Ƃ��l����B462��110�̗����������f���̂����ő�̂��̂�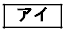 �ł���B
�ł���B
�Ԃ������`����ׂč�邱�Ƃ��ł��鐳���`�̂����A�ӂ̒������ŏ��ł�����̂́A��ӂ̒�����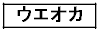 �̂��̂ł���B
�̂��̂ł���B
�܂��A�Ԃ������`����ׂĐ����`�ł͂Ȃ������`�����Ƃ��A���̒����Əc�̒����̍��̐�Βl���ŏ��ɂȂ�̂́A462�̖�110�̖��l����ƁA���̐�Βl�� �ɂȂ�Ƃ��ł��邱�Ƃ��킩��B
�ɂȂ�Ƃ��ł��邱�Ƃ��킩��B
�c�̒��������̒������ ���������`�̂����A���̒������ŏ��ł�����̂́A���̒�����
���������`�̂����A���̒������ŏ��ł�����̂́A���̒����� �̂��̂ł���B
�̂��̂ł���B
 (2) �Ԏq����Ƒ��Y����́A(1)�ŗp�����Ԃ������`��1���ȏ���ׂĒ����`�����A���̉E���ɉ��̒�����363�ŏc�̒�����154�ł���������`��1���ȏ���ׂāA�}2�̂悤�Ȑ����`�Ⓑ���`����邱�Ƃ��l���Ă���B
(2) �Ԏq����Ƒ��Y����́A(1)�ŗp�����Ԃ������`��1���ȏ���ׂĒ����`�����A���̉E���ɉ��̒�����363�ŏc�̒�����154�ł���������`��1���ȏ���ׂāA�}2�̂悤�Ȑ����`�Ⓑ���`����邱�Ƃ��l���Ă���B���̂Ƃ��A�Ԃ������`����ׂĂł��钷���`�̏c�̒����ƁA�������`����ׂĂł��钷���`�̏c�̒����͓������B����āA�}2�̂悤�Ȓ����`�̂����A�c�̒������ŏ��̂��̂́A�c�̒����� �̂��̂ł���A�}2�̂悤�Ȓ����`�͏c�̒�����
�̂��̂ł���A�}2�̂悤�Ȓ����`�͏c�̒�����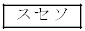 �̔{���ł���B
�̔{���ł���B
��l�́A���̂悤�ɘb���Ă���B
�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�| �Ԏq�F�Ԃ������`�Ɛ������`��}2�̂悤�ɕ��ׂĐ����`������Ă݂悤��B
���Y�F�Ԃ������`�̉��̒�����462�Ő������`�̉��̒�����363������A�}2�̂悤�Ȑ����`�̉��̒�����462��363��g�ݍ��킹�č�邱�Ƃ��ł��钷���łȂ��Ƃ����Ȃ��ˁB
�Ԏq�F�����`������A���̒�����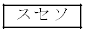 �̔{���ł��Ȃ��Ƃ����Ȃ��ˁB
�̔{���ł��Ȃ��Ƃ����Ȃ��ˁB �|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|462��363�̍ő���� �ł���A
�ł���A �̔{���̂�����
�̔{���̂�����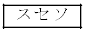 �̔{���ł�����ŏ��̐��̐�����
�̔{���ł�����ŏ��̐��̐����� �ł���B
�ł���B
�����̂��ƂƁA�g�������`�̖������Ԃ������`���������`��1���ȏ�ł��邱�Ƃ���A�}2�̂悤�Ȑ����`�̂����A�ӂ̒������ŏ��ł�����̂́A��ӂ̒����� �̂��̂ł��邱�Ƃ��킩��B
�̂��̂ł��邱�Ƃ��킩��B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@���Ă����ۂ��Ő��������Ȃ��悤�ɂ��邽�߂��A�e�ӂ̒�����11���������Ă��ĉ��傫�Ȑ��ɂȂ�悤�ɍ�₳��Ă���(�ŏ��̃A�C�Œ��ӊ��N���Ă���)�̂ŁA�������Ȃ��悤�ɒ��ӂ��K�v�ł��B
(1)�@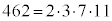 �C
�C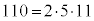 (�������Q��)�̗����������ő�̑f����11�ł��B�@�A�C 11 ......[��]
(�������Q��)�̗����������ő�̑f����11�ł��B�@�A�C 11 ......[��]
�Ԃ������`���c��x�A����y���ׂ�Ƃ��āA�����`�ɂȂ邽�߂ɁA
��������ŏ��̎��R���̑gx�Cy�́A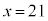 �C
�C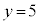 �C��ӂ̒����́A
�C��ӂ̒����́A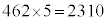 �@�E�G�I�J 2310 ......[��]�����`�łȂ������`�����Ƃ��A���̒����Əc�̒����̍��̐�Βl���ŏ��ɂȂ�̂́A���̐�Βl���A462��110�̍ő����22 (�������Q��)�ɂȂ�Ƃ��ł��B�@�L�N 22 ......[��]�Ԃ������`���c��x�A����y���ׂ�Ƃ��āA�c�̒��������̒������22�����Ƃ��A
�@�E�G�I�J 2310 ......[��]�����`�łȂ������`�����Ƃ��A���̒����Əc�̒����̍��̐�Βl���ŏ��ɂȂ�̂́A���̐�Βl���A462��110�̍ő����22 (�������Q��)�ɂȂ�Ƃ��ł��B�@�L�N 22 ......[��]�Ԃ������`���c��x�A����y���ׂ�Ƃ��āA�c�̒��������̒������22�����Ƃ��A ���ӂ�22�Ŋ����āA
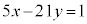 �@����@
�@����@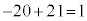 �Ȃ̂ŁA�@����������Ƃ���
�Ȃ̂ŁA�@����������Ƃ���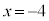 �C
�C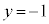 ���A
���A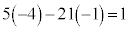 �@����A
�@����A
�@�|�A���A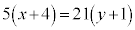 5��21�݂͌��ɑf�Ȃ̂ŁAk�𐮐��Ƃ��āA
5��21�݂͌��ɑf�Ȃ̂ŁAk�𐮐��Ƃ��āA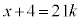 �C
�C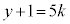
����āA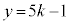 �ł����A�ŏ��ƂȂ鎩�R��y�́A
�ł����A�ŏ��ƂȂ鎩�R��y�́A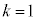 �̂Ƃ�
�̂Ƃ�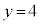
�����`�̉��̒����́A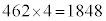 �@�P�R�T�V 1848 ......[��]
�@�P�R�T�V 1848 ......[��]
(���̂Ƃ�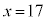 �Ȃ̂ŁA�c�̒����́A
�Ȃ̂ŁA�c�̒����́A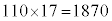 �ł�)
�ł�)
(2) �Ԃ������`���c��x���ׂ��Ƃ��̏c�̒���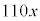 �ƁA�������`���c��y���ׂ��Ƃ��̏c�̒���
�ƁA�������`���c��y���ׂ��Ƃ��̏c�̒���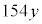 ���������A
���������A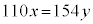
���ӂ�22�Ŋ����āA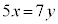 5��7�݂͌��ɑf�Ȃ̂ŁA�c�̒������ŏ��ɂȂ�Ƃ��A
5��7�݂͌��ɑf�Ȃ̂ŁA�c�̒������ŏ��ɂȂ�Ƃ��A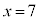 �C
�C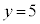
���̂Ƃ��̏c�̒����́A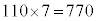 �@�X�Z�\ 770 ......[��]
�@�X�Z�\ 770 ......[��]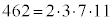 ��
��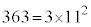 �̍ő���́A
�̍ő���́A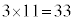 �ł��B�@�^�` 33 ......[��]
�ł��B�@�^�` 33 ......[��]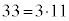 �̔{���̂����ŁA
�̔{���̂����ŁA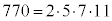 �̔{���ł�����ŏ��̐��̐����A�����A�ŏ����{���́A
�̔{���ł�����ŏ��̐��̐����A�����A�ŏ����{���́A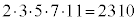 �@�c�e�g�i 2310 ......[��]�}2�̂悤�Ȑ����`�ɂ����āA�c�̒�����770�̔{���ŁAx�����R���Ƃ���
�@�c�e�g�i 2310 ......[��]�}2�̂悤�Ȑ����`�ɂ����āA�c�̒�����770�̔{���ŁAx�����R���Ƃ���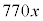 �Ƃ���ƁA���̒����́A�Ԃ������`��y���ɕ��ׁA�������`��z���ׂ�Ƃ��āA
�Ƃ���ƁA���̒����́A�Ԃ������`��y���ɕ��ׁA�������`��z���ׂ�Ƃ��āA ���ӂ�11�Ŋ���ƁA
70��3�݂͌��ɑf�Ȃ̂ŁAx��3�̔{���ŁAk�����R���Ƃ��āA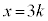 �Ƃ����ƁA
�Ƃ����ƁA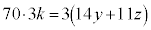 �@��
�@�� 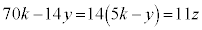
14��11�݂͌��ɑf�Ȃ̂ŁAz��14�̔{���ŁA���̂����ŏ����̂�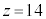
���̂Ƃ��A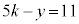 �C�܂�A
�C�܂�A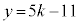
�ŏ��ƂȂ�y�́A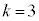 �̂Ƃ�
�̂Ƃ�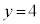 �C�܂�
�C�܂�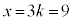
����āA�����`��1�ӂ̒����́A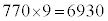 �@�j�k�l�m 6930 ......[��]
�@�j�k�l�m 6930 ......[��]
(���̂Ƃ��A�Ԃ������`��4���ɕ��ׂĒ���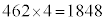 �C�������`��14���ɕ��ׂĒ���
�C�������`��14���ɕ��ׂĒ���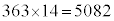 �C
�C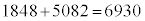 �ƂȂ��Ă��܂�)
�ƂȂ��Ă��܂�)
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B