�@���ʃe�X�g���wIA '24�N��5��@
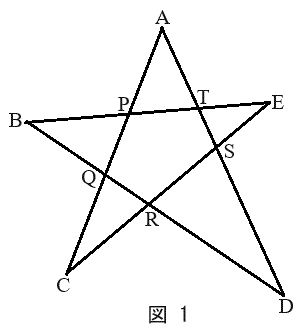 �}1�̂悤�ɁA���ʏ��5�_A�CB�CC�CD�CE������A����AC�CCE�CEB�CBD�CDA�ɂ���āA���`�̐}�`���ł���Ƃ����l����B����AC��BE�̌�_��P�CAC��BD�̌�_��Q�CBD��CE�̌�_��R�CAD��CE�̌�_��S�CAD��BE�̌�_��T�Ƃ���B
�}1�̂悤�ɁA���ʏ��5�_A�CB�CC�CD�CE������A����AC�CCE�CEB�CBD�CDA�ɂ���āA���`�̐}�`���ł���Ƃ����l����B����AC��BE�̌�_��P�CAC��BD�̌�_��Q�CBD��CE�̌�_��R�CAD��CE�̌�_��S�CAD��BE�̌�_��T�Ƃ���B
�����ł�
AP�FPQ�FQC = 2�F3�F3�CAT�FTS�FSD = 1�F1�F3
�������`�̐}�`���l����B
�ȉ��̖��ɂ����Ĕ������ꍇ�́A�ł��ȒP�Ȑ����̔�œ�����B
(1) ��AQD�ƒ���CE�ɒ��ڂ����
�����藧�̂�
QR�FRD =  �F
�F
�ƂȂ�B�܂��A��AQD�ƒ���BE�ɒ��ڂ����
QB�FBD =  �F
�F
�ƂȂ�B����������
�ƂȂ邱�Ƃ��킩��B
 �̉Q
�̉Q
 �@AC�@�@
�@AC�@�@ �@AP�@�@
�@AP�@�@ �@AQ�@�@
�@AQ�@�@ �@CP�@�@
�@CP�@�@ �@PQ
�@PQ
(2) 5�_P�CQ�CR�CS�CT������~����ɂ���Ƃ��A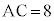 �ł���Ƃ���B
�ł���Ƃ���B (i) 5�_A�CP�CQ�CS�CT�ɒ��ڂ���ƁAAT�FAS = 1�F2���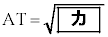 �ƂȂ�B����ɁA5�_D�CQ�CR�CS�CT�ɒ��ڂ����
�ƂȂ�B����ɁA5�_D�CQ�CR�CS�CT�ɒ��ڂ����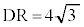 �ƂȂ邱�Ƃ��킩��B
�ƂȂ邱�Ƃ��킩��B (ii) 3�_A�CB�CC��ʂ�~�Ɠ_D�Ƃ̈ʒu�W���A�����\�z�Ɋ�Â��Ē��ׂ悤�B
�|�\�z�|�|�|�|�|�|�|�|�|�|�|�|�|
����AC��BD�̌�_Q�ɒ��ڂ��A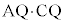 ��
��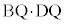 �̑召���ׂ�B
�̑召���ׂ�B �|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|
�܂��A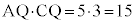 ����
����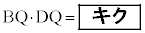 �ł��邱�Ƃ���
�ł��邱�Ƃ��� 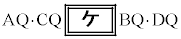 �@����@
�@����@�����藧�B�܂��A3�_A�CB�CC��ʂ�~�ƒ���BD�Ƃ̌�_�̂����AB�ƈقȂ�_��X�Ƃ����
 �@����A
�@����A�����藧�B�@�ƇA�̍��ӂ͓����Ȃ̂ŁA�@�ƇA�̉E�ӂ��ׂ邱�Ƃɂ��A ��������B���������āA�_D��3�_A�CB�CC��ʂ�~��
��������B���������āA�_D��3�_A�CB�CC��ʂ�~�� �ɂ���B
�ɂ���B
 �`
�`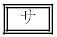 �̉Q(�������̂��J��Ԃ��I��ł��悢�B)
�̉Q(�������̂��J��Ԃ��I��ł��悢�B) �@���@�@
�@���@�@ �@���@�@
�@���@�@ �@��
�@��
 �̉Q
�̉Q
 �@�����@�@
�@�����@�@ �@����@�@
�@����@�@ �@�O��
�@�O��
(iii) 3�_C�CD�CE��ʂ�~��2�_A�CB�Ƃ̈ʒu�W�ɂ��Ē��ׂ悤�B
���̐��`�̐}�`�ɂ����āA�����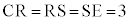 �ƂȂ邱�Ƃ��킩��B���������āA�_A��3�_C�CD�CE��ʂ�~��
�ƂȂ邱�Ƃ��킩��B���������āA�_A��3�_C�CD�CE��ʂ�~�� �ɂ���A�_B��3�_C�CD�CE��ʂ�~��
�ɂ���A�_B��3�_C�CD�CE��ʂ�~��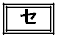 �ɂ���B
�ɂ���B
 �C
�C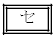 �̉Q(�������̂��J��Ԃ��I��ł��悢�B)
�̉Q(�������̂��J��Ԃ��I��ł��悢�B) �@�����@�@
�@�����@�@ �@����@�@
�@����@�@ �@�O��
�@�O��
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@���l���E�X�̒藝�A���ׂ��̒藝���劈����ł��B
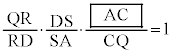
(1) ���l���E�X�̒藝��K�p����̂ł����A��ACS�Ɓ�AQD�����_A�����L����悤�ɏd�Ȃ��Ă�����������܂��BA���o�����āAA��C��Q��R��D��S��A�̂悤�ɉ��܂��B���l���E�X�̒藝���A
 �@�A 0 ......[��]
�@�A 0 ......[��]�� 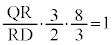
QR�FRD = 1�F4�@�C 1�@�E 4 ......[��]
��AQD�Ɓ�BDT�����_D�����L����悤�ɏd�Ȃ��Ă�����������܂��BD���o�����āAD��B��Q��P��A��T��D�̂悤�ɉ��܂��B���l���E�X�̒藝���A
�� 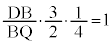
QB�FBD = 3�F8�@�G 3�@�I 8 ......[��]
�]���āABQ�FQR�FRD = 3�F1�F4
�� 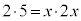 �C
�C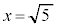 �@�J 5 ......[��]
�@�J 5 ......[��]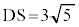 �C
�C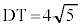 �@����B
�@����B
����ɁA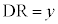 �Ƃ�����
�Ƃ�����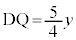 �A���ׂ��̒藝���A
�A���ׂ��̒藝���A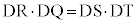
�� 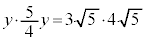 �C
�C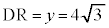 �@����C
�@����C
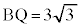 �C
�C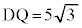 �C
�C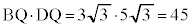 �@�L�N 45 ......[��]
�@�L�N 45 ......[��] 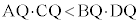 �@�P 0 ......[��]�@����@
�@�P 0 ......[��]�@����@�~����̓_A�CB�CC�CX�ɂ��āA��AC�ƌ�BX�̌�_��Q�Ȃ̂ŁA���ׂ��̒藝���A
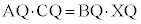 �@����A�@�R 1 ......[��]
�@����A�@�R 1 ......[��]�@�C�A���A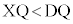 �@�T 0 ......[��]�]���āA�_D��3�_A�CB�CC��ʂ�(�_X���ʂ�)�~�̊O���ɂ���܂��B�@�V 2 ......[��]
�@�T 0 ......[��]�]���āA�_D��3�_A�CB�CC��ʂ�(�_X���ʂ�)�~�̊O���ɂ���܂��B�@�V 2 ......[��]
3�_C�CD�CE��ʂ�~�ƒ���AD�Ƃ̌�_�̂���D�ƈقȂ�_��Y�Ƃ���ƁA�~����̓_C�CD�CE�CY�ɂ��āA��CE�ƌ�DY�̌�_��S�Ȃ̂ŁA���ׂ��̒藝���A 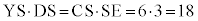 �@(�� ��蕶)
�@(�� ��蕶)�B���A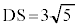 �C����āA
�C����āA �_A��3�_C�CD�CE��ʂ�~�̊O���ɂ���܂��B�@�X 2 ......[��]
3�_C�CD�CE��ʂ�~�ƒ���BD�Ƃ̌�_�̂���D�ƈقȂ�_��Z�Ƃ���ƁA�~����̓_C�CD�CE�CZ�ɂ��āA��CE�ƌ�DZ�̌�_��R�Ȃ̂ŁA���ׂ��̒藝���A
�C���A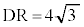 �C�܂��A
�C�܂��A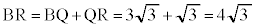 �C����āA
�C����āA �_A��3�_C�CD�CE��ʂ�~�̊O���ɂ���܂��B�@�Z 2 ......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 

 �@�A 0 ......[��]
�@�A 0 ......[��]