�@�Z���^�[�������wIIB 2011�N���@
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
[1][1]�@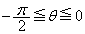 �̂Ƃ��A��
�̂Ƃ��A��
�̍ŏ��l�����߂悤�B
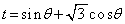 �Ƃ�����
�Ƃ����� �ł��邩��
�ƂȂ�B�܂�
�ł���B
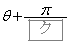 �̂Ƃ蓾��l�͈̔͂�
�̂Ƃ蓾��l�͈̔͂� �ł��邩��At �̂Ƃ蓾��l�͈̔͂�
�ł���B���������āAy�� �C���Ȃ킿
�C���Ȃ킿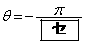 �̂Ƃ��A�ŏ��l
�̂Ƃ��A�ŏ��l ���Ƃ�B
���Ƃ�B
[2]�@���R��x�ŁA����
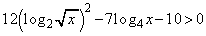 �@�@����@
�@�@����@
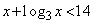 �@�@����A
�@�@����A�������̂����߂悤�B
�܂��Ax�𐳂̎����Ƃ��āA�����@���l����B�@��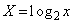 �Ƃ�����
�Ƃ����� �ƂȂ�B����2����������������
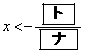 �C
�C
�ƂȂ�B���������āA�����@�����ŏ��̎��R��x�� �ł���A
�ł���A �ȏ�̂��ׂĂ̎��R��x�͇@�����B
�ȏ�̂��ׂĂ̎��R��x�͇@�����B
���ɁA�����A�ɂ��čl����ƁA�A�����ő�̎��R��x��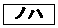 �ł���A
�ł���A �ȉ��̂��ׂĂ̎��R��x�͇A�����B
�ȉ��̂��ׂĂ̎��R��x�͇A�����B
���������āA���߂�x�� �ȏ�
�ȏ� �ȉ��̎��R���ł���B
�ȉ��̎��R���ł���B [��]
[2]�@���W���ʏ�ŁA������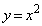 ��C�Ƃ���B
��C�Ƃ���B
�Ȑ�C��̓_P��x���W��a�Ƃ���B�_P�ɂ�����C�̐ڐ�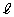 �̕�������
�̕�������
�ł���B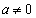 �̂Ƃ�����
�̂Ƃ�����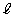 ��x���ƌ����_��Q�Ƃ���ƁAQ�̍��W��
��x���ƌ����_��Q�Ƃ���ƁAQ�̍��W��
�ł���B
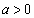 �̂Ƃ��A�Ȑ�C�ƒ���
�̂Ƃ��A�Ȑ�C�ƒ���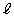 �����x���ň͂܂ꂽ�}�`�̖ʐς�S�Ƃ����
�����x���ň͂܂ꂽ�}�`�̖ʐς�S�Ƃ����
�ł���B
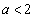 �̂Ƃ��A�Ȑ�C�ƒ���
�̂Ƃ��A�Ȑ�C�ƒ���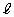 ����ђ���
����ђ���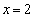 �ň͂܂ꂽ�}�`�̖ʐς�T�Ƃ����
�ň͂܂ꂽ�}�`�̖ʐς�T�Ƃ����
�ł���B
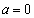 �̂Ƃ���
�̂Ƃ���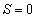 �C
�C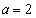 �̂Ƃ���
�̂Ƃ���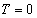 �ł���Ƃ��āA
�ł���Ƃ��āA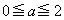 �ɑ���
�ɑ���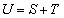 �Ƃ����Ba�����͈̔͂��Ƃ��AU��
�Ƃ����Ba�����͈̔͂��Ƃ��AU��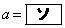 �ōő�l
�ōő�l ���Ƃ�A
���Ƃ�A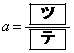 �ōŏ��l
�ōŏ��l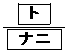 ���Ƃ�B
���Ƃ�B
[��]
[3]�@��������œ_P�Ɏ���a���Ή����Ă���Ƃ��Aa��_P�̍��W�Ƃ����A���W��a�ł���_P��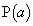 �ŕ\���B
�ŕ\���B
��������ɓ_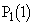 �C
�C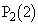 ���Ƃ�B����
���Ƃ�B����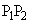 ��3�F1�ɓ�������_��
��3�F1�ɓ�������_��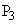 �Ƃ���B��ʂɁA���R��n�ɑ��āA����
�Ƃ���B��ʂɁA���R��n�ɑ��āA����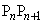 ��3�F1�ɓ�������_��
��3�F1�ɓ�������_��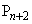 �Ƃ���B�_
�Ƃ���B�_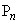 �̍��W��
�̍��W��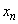 �Ƃ���B
�Ƃ���B
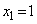 �C
�C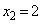 �ł���A
�ł���A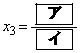 �ł���B����
�ł���B����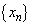 �̈�ʍ������߂邽�߂ɁA���̐���̊K��������l���悤�B���R��n�ɑ���
�̈�ʍ������߂邽�߂ɁA���̐���̊K��������l���悤�B���R��n�ɑ���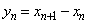 �Ƃ���B
�Ƃ���B
�ł���B���������āA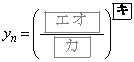 �@(
�@(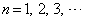 )�ł���A
)�ł���A
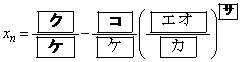 �@(
�@(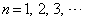 )
)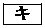 �C
�C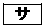 �ɂ��ẮA���Ă͂܂���̂��A����
�ɂ��ẮA���Ă͂܂���̂��A���� �`
�` �̂����������I�ׁB�������̂��J��Ԃ��I��ł��悢�B
�̂����������I�ׁB�������̂��J��Ԃ��I��ł��悢�B

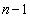 �@�@
�@�@
 �@�@
�@�@
 �@�@
�@�@
���ɁA���R��n�ɑ���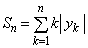 �����߂悤�B
�����߂悤�B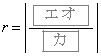 �Ƃ�����
�Ƃ�����
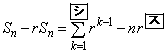 �@(
�@(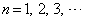 )
)
�ƂȂ�B�������A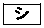 �C
�C �C
�C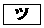 �C
�C �ɂ��ẮA���Ă͂܂���̂��A����
�ɂ��ẮA���Ă͂܂���̂��A���� �`
�` �̂����������I�ׁB�������̂��J��Ԃ��I��ł��悢�B
�̂����������I�ׁB�������̂��J��Ԃ��I��ł��悢�B

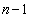 �@�@
�@�@
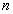 �@�@
�@�@
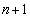 �@�@
�@�@
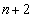
[��]
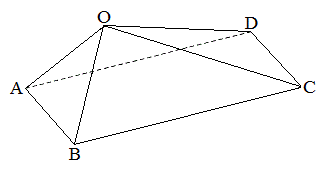 [4]�@�l�p��OABCD�ɂ����āA�O�p�`OBC�ƎO�p�`OAD�͍����ŁA
[4]�@�l�p��OABCD�ɂ����āA�O�p�`OBC�ƎO�p�`OAD�͍����ŁA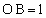 �C
�C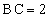 �C
�C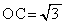 �ł���A��ʂ̎l�p�`ABCD�͒����`�ł���A
�ł���A��ʂ̎l�p�`ABCD�͒����`�ł���A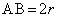 �Ƃ����A
�Ƃ����A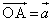 �C
�C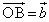 �C
�C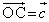 �Ƃ����B
�Ƃ����B
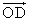 ��
��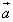 �C
�C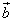 �C
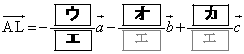
�C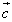 ��p���ĕ\����
��p���ĕ\����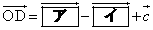 �ł���B��OD��1�F2�ɓ�������_��L�Ƃ����
�ł���B��OD��1�F2�ɓ�������_��L�Ƃ����
�ƂȂ�B
����ɕ�OB�̒��_��M�C3�_A�CL�CM�̒�߂镽�ʂ�α�Ƃ��A����α�ƕ�OC�Ƃ̌�_��N�Ƃ���B�_N�͕���α��ɂ��邱�Ƃ���A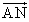 �͎���s�Ct��p����
�͎���s�Ct��p����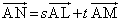 �ƕ\�����̂ŁA
�ƕ\�����̂ŁA
�ƂȂ�B����A�_N�͕�OC��ɂ�����B����炩��A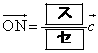 �ƂȂ�B
�ƂȂ�B
�܂��A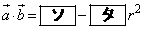 �C
�C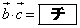 �C
�C �ł���B����āA
�ł���B����āA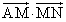 ���v�Z����ƁA
���v�Z����ƁA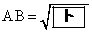 �̂Ƃ��A����AM�ƒ���MN�͐����ɂȂ邱�Ƃ��킩��B
�̂Ƃ��A����AM�ƒ���MN�͐����ɂȂ邱�Ƃ��킩��B
[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 
 �C
�C
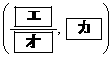
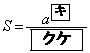

 ���Ƃ�A
���Ƃ�A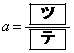 �ōŏ��l
�ōŏ��l ���Ƃ�B
���Ƃ�B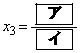 �ł���B����
�ł���B����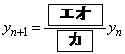 �@(
�@( �@(
�@( �@(
�@( �Ƃ�����
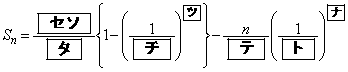
�Ƃ�����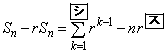 �@(
�@(
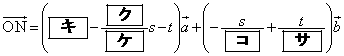
 �ƂȂ�B
�ƂȂ�B