センター数学IIB '11年第2問
座標平面上で、放物線 をCとする。
をCとする。
曲線C上の点Pのx座標をaとする。点PにおけるCの接線 の方程式は
の方程式は
である。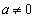 のとき直線
のとき直線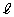 がx軸と交わる点をQとすると、Qの座標は
がx軸と交わる点をQとすると、Qの座標は
である。
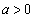 のとき、曲線Cと直線
のとき、曲線Cと直線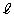 およびx軸で囲まれた図形の面積をSとすると
およびx軸で囲まれた図形の面積をSとすると
である。
 のとき、曲線Cと直線
のとき、曲線Cと直線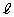 および直線
および直線 で囲まれた図形の面積をTとすると
で囲まれた図形の面積をTとすると
である。
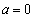 のときは
のときは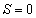 ,
,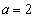 のときは
のときは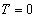 であるとして、
であるとして、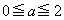 に対して
に対して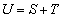 とおく。aがこの範囲を動くとき、Uは
とおく。aがこの範囲を動くとき、Uは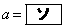 で最大値
で最大値 をとり、
をとり、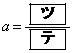 で最小値
で最小値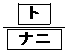 をとる。
をとる。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
解答 センター試験の微積の問題としては、この程度が適切だと思います。以前の複雑で面倒な計算をさせる問題では何を試験したいのかわからなくなります。今後も、今年の方針を継続することを期待します。
C:
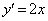
点P における接線
における接線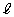 は、
は、
 :
: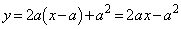
 直線
直線 がx軸と交わる点Qは、
がx軸と交わる点Qは、 として、
として、
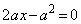 ∴
∴ 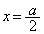

(エ) a (オ) 2 (カ) 0 ......[答]
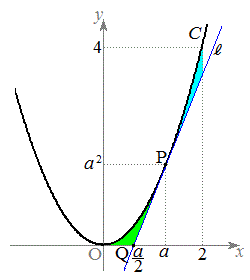
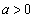 のとき、曲線Cと直線
のとき、曲線Cと直線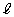 およびx軸で囲まれた図形は、右図黄緑色着色部です。この面積Sは、
およびx軸で囲まれた図形は、右図黄緑色着色部です。この面積Sは、
(キ) 3 (ク) 1 (ケ) 2 ......[答]
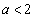 のとき、曲線Cと直線
のとき、曲線Cと直線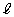 および直線
および直線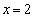 で囲まれた図形は、右図水色着色部です。この面積Tは、
で囲まれた図形は、右図水色着色部です。この面積Tは、
(コ) 3 (サ) 2 (シ) 4 (ス) 8 (セ) 3 ......[答]
問題文に、「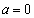 のときは
のときは ,
,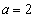 のときは
のときは 」という記述が見えます。ここで、S,Tの結果を確認してから先に進むようにしましょう。
」という記述が見えます。ここで、S,Tの結果を確認してから先に進むようにしましょう。
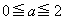 に対して
に対して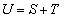 とおくと、
とおくと、
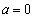 のとき
のとき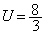 ,
, のとき
のとき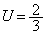 ,
,
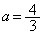 のとき
のとき
増減表より、Uは、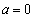 で最大値
で最大値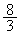 をとり、
をとり、 で最小値
で最小値 をとります(3次関数の最大・最小を参照)。
をとります(3次関数の最大・最小を参照)。
(ソ) 0 (タ) 8 (チ) 3 (ツ) 4 (テ) 3 (ト) 8 (ナ) 2 (ニ) 7 ......[答]
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 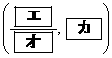
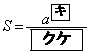

 をとり、
をとり、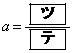 で最小値
で最小値 をとる。
をとる。