3次関数の最大・最小 関連問題
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
例1.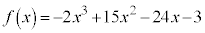 の
の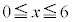 における最大値と最小値を求める。
における最大値と最小値を求める。
[解答] 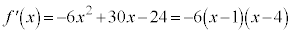 (微分を参照)
(微分を参照)
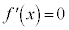 とすると、
とすると、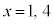
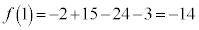 :極小値
:極小値
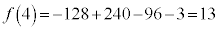 :極大値
:極大値
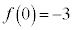 :区間の左端での関数値
:区間の左端での関数値
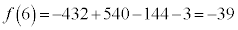 :区間の右端での関数値
:区間の右端での関数値
増減表は(3次関数の増減を参照)、
以上より、最大値: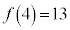 ,最小値:
,最小値: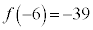 ......[答]
......[答]
例2.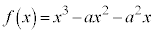 の
の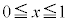 における最大値と最小値を求める。
における最大値と最小値を求める。
[解答] 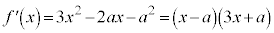
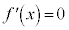 とすると、
とすると、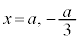 ですが、aと
ですが、aと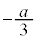 の大小関係は不明です。このときには、
の大小関係は不明です。このときには、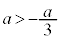 となる場合、
となる場合、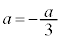 となる場合、
となる場合、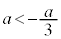 となる場合に、分けて考える必要があります。
となる場合に、分けて考える必要があります。
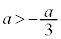 となるのは、
となるのは、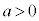 のときです。
のときです。
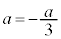 となるのは、
となるのは、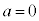 のときです。
のときです。
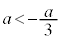 となるのは、
となるのは、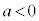 のときです。
のときです。
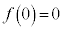 ,
,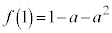 ,
,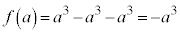 ,
,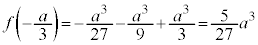
(i) 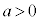 のとき、
のとき、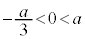 ですが、
ですが、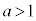 か
か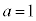 か
か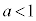 か不明です。これも場合分けして考える必要があります。
か不明です。これも場合分けして考える必要があります。
(i-1) 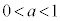 のとき、
のとき、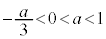 で、増減表は以下のようになります。
で、増減表は以下のようになります。
増減表から、最小値: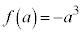 になることはわかりますが、0と
になることはわかりますが、0と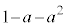 の大小関係がわかりません。
の大小関係がわかりません。
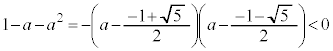 とすると、
とすると、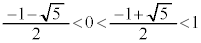 なので、
なので、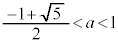 です。
です。
そこで、さらに場合分けが必要で、
(i-1-1) 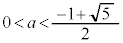 のとき、
のとき、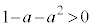 なので、最大値:
なので、最大値: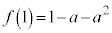 です。
です。
(i-1-2) 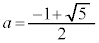 のとき、
のとき、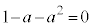 なので、最大値:
なので、最大値: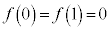 です。
です。
(i-1-3) 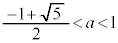 のとき、
のとき、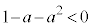 なので、最大値:
なので、最大値: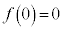 です。
です。
(i-2) 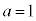 のとき、
のとき、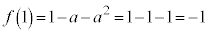 ,増減表は以下のようになります。
,増減表は以下のようになります。
最大値: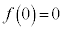 ,最小値:
,最小値: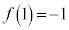 です。
です。
(i-3) 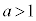 のとき、増減表は以下のようになります。
のとき、増減表は以下のようになります。
最大値: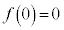 ,最小値:
,最小値: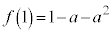 です。
です。
(ii) 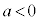 のとき、
のとき、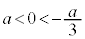 ですが、
ですが、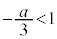 か
か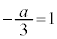 か
か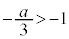 か不明です。
か不明です。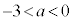 ,
,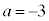 ,
,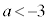 に場合分けして考えます。
に場合分けして考えます。
(ii-1) 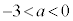 のとき、
のとき、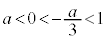 で増減表は以下のようになります。
で増減表は以下のようになります。
(i-1)と同様の場合分けを行いますが、今度は、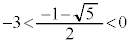 なので、以下のような場合分けとなります。
なので、以下のような場合分けとなります。
(ii-1-1) 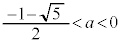 のとき、
のとき、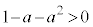 なので、最大値:
なので、最大値: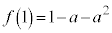 ,最小値:
,最小値: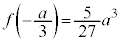
(ii-1-2) 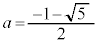 のとき、
のとき、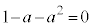 なので、最大値:
なので、最大値: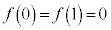 ,最小値:
,最小値: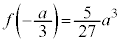
(ii-1-3) 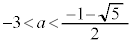 のとき、
のとき、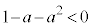 なので、最大値:
なので、最大値: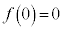 ,最小値:
,最小値: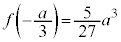
(ii-2) 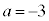 のとき、
のとき、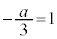 ですが、
ですが、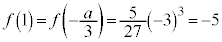 で、増減表は以下のようになります。
で、増減表は以下のようになります。
最大値: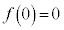 ,最小値:
,最小値: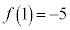 です。
です。
(ii-3) 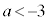 のとき、
のとき、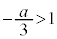 ,増減表は以下の通り。
,増減表は以下の通り。
最大値: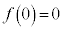 ,最小値:
,最小値: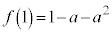
(iii) 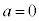 のとき、
のとき、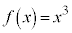 は
は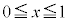 において単調増加で、最大値:
において単調増加で、最大値: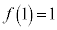 ,最小値:
,最小値: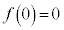
以上をまとめると、
最大値: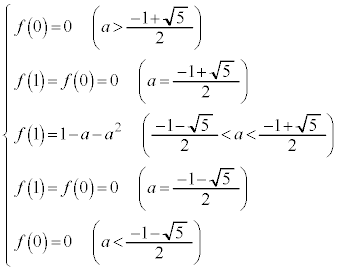 ,最小値:
,最小値: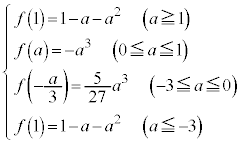 ......[答]
......[答]
3次関数の最大・最小(2)に続く。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
数学基礎事項TOP 数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 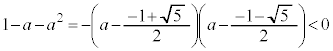 とすると、
とすると、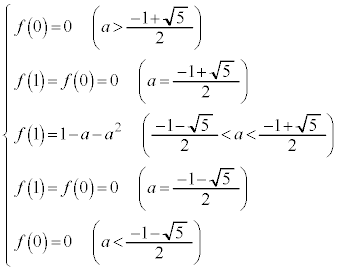 ,最小値:
,最小値: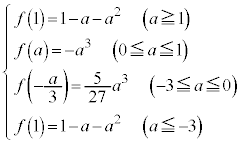 ......[答]
......[答]