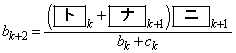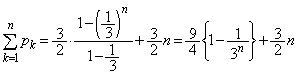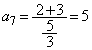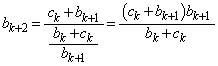センター数学IIB '13年第3問
(1) 数列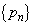
は次を満たすとする。 数列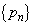
の一般項と、初項から第n項までの和を求めよう。まず、①から 
(
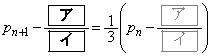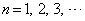)となるので、数列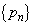
の一般項は である。したがって、自然数nに対して
である。
(2) 正の数からなる数列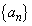
は、初項から第3項が
，
，
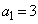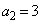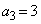であり、すべての自然数nに対して 
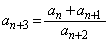･･･②を満たすとする。また、数列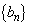
，
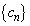を、自然数nに対して、
，
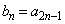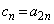で定める。数列
，
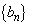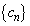の一般項を求めよう。まず、②から である。したがっ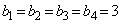て、
となるので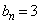 
(
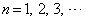) ･･･③と推定できる。
③を示すためには、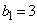
から、すべての自然数nに対して 
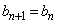･･･④であることを示せば良い。このことを「まず、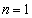
のとき④が成り立つことを示し、次に、
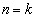のとき④が成り立つと仮定すると、
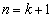のときも④が成り立つことを示す方法」を用いて証明しよう。この方法を
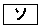という。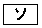
に当てはまるものを、次の
～
のうちから一つ選べ。
組立除法 
弧度法 
数学的帰納法 背理法
[Ⅱ]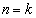 
のとき、④が成り立つ、すなわち、 
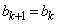･･･⑤と仮定する。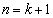
のとき、②のnに
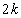を代入して得られる等式と、
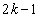を代入して得られる等式から 
，
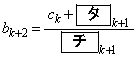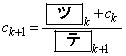
となるので、
は と表される。したがって、⑤により、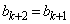
が成り立つので、④は
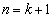のときにも成り立つ。[Ⅰ]，[Ⅱ]により、すべての自然数nに対して④の成り立つことが証明された。
したがって、③が成り立つので、数列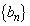
の一般項は
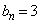である。
次に、②のnを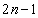
に置き換えて得られる等式と③から となり、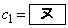
であることと①から、数列
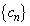の一般項は、(1)で求めた数列
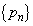の一般項と等しくなることがわかる。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
解答 数列は、標準的な2項間漸化式の問題です。数学的帰納法の部分は実は極めて易しいのですが、センター試験のためだけの設問の仕方がユニークで、面食らった受験生もいたと思われます。
(1) 
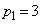
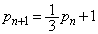･･･⑥
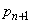と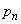
をαに置き換えると、
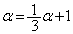･･･⑦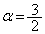
⑥－⑦より、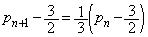
(ア) 3 (イ) 2 ......[答]数列
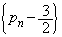は、初項
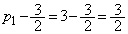，公比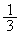
の等比数列です。 ∴ 
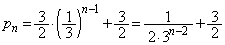
(ウ) 2 (エ) 3 (オ) 3 (カ) 2 ......[答] (キ) 9 (ク) 4 (ケ) 3 (コ) 3 (サ) 2 ......[答]
②から
(シ) 2 (ス) 5 (セ) 3 ......[答]これで、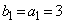
，
，
，
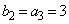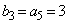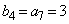となり、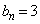
(
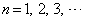) ･･･③ と推定できます。
③を示すためには、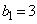
から、すべての自然数nに対して 
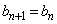･･･④であることを示せば良いのですが、「まず、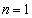
のとき④が成り立つことを示し、次に、
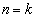のとき④が成り立つと仮定すると、
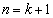のときも④が成り立つことを示す方法」は、数学的帰納法です。(ソ) ......[答] [Ⅰ] 
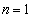のとき、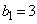
，
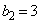であることから④は成り立ちます。 [Ⅱ]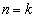 
のとき、④が成り立つ、すなわち、 
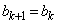･･･⑤と仮定します。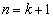
のとき、②のnに
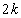を代入して得られる等式 と、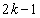
を代入して得られる等式 から
，
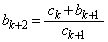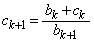
(タ) b (チ) c (ツ) b (テ) b ......[答]
これより、
(ト) c (ナ) b (ニ) b ......[答]したがって、⑤により、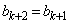
が成り立つので、
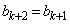となり、④は
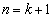のときにも成り立ちます。 [Ⅰ]，[Ⅱ]により、すべての自然数nに対して④の成り立つことが証明されました。
したがって、③が成り立つので、数列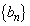
の一般項は
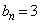です。
また、 (ヌ) 3 ......[答]
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中！理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。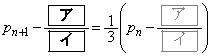 
，
(
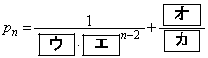
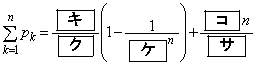
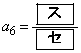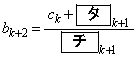) ･･･①
，
，
，
のとき、
，
であることから④は成り立つ。
，
，
･･･②
，
，
，
，
