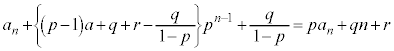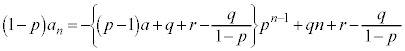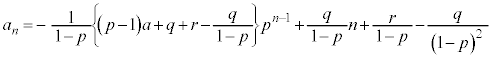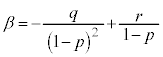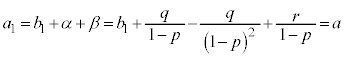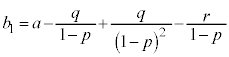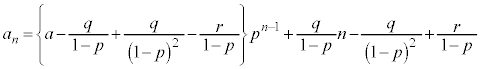2項間漸化式 関連問題
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
数列の隣接2項: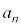 ,
,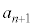 に関する関係式を2項間漸化式と言います。
に関する関係式を2項間漸化式と言います。
(1) 基本形: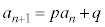 (p,q:定数,
(p,q:定数,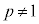 とする。
とする。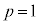 のときは等差数列)
のときは等差数列)
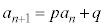 ・・・① (
・・・① (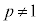 ,
,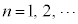 ),
),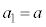 とする。
とする。
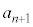 ,
,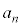 をともにxとおいた1次方程式:
をともにxとおいた1次方程式: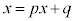 ・・・② を解くと、
・・・② を解くと、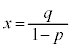
①-②より、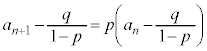
これより、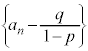 は、初項:
は、初項: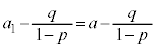 ,公比:pの等比数列。
,公比:pの等比数列。
よって、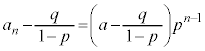
∴ 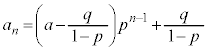
[注意] 結果を暗記しても何の意味もありません。道すじを覚えること。
2項間漸化式にはさまざまな亜種があります。ここでは、代表的な2例をあげておきます。
(2) 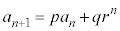 (p,q,r:定数,
(p,q,r:定数,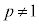 )
)
基本形(1)で定数qだったところが、等比数列の形をしているタイプです。
両辺を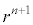 で割る(
で割る(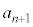 がいるときは、
がいるときは、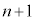 乗で割ると覚えてください)と、
乗で割ると覚えてください)と、
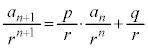
ここで、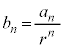 とおくと、
とおくと、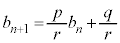
これは、2項間漸化式の基本形です。(1)の手順で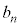 を求めて、
を求めて、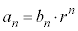 とすれば一般項が求められます。
とすれば一般項が求められます。
(3) 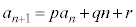 (p,q,r:定数,
(p,q,r:定数,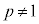 )
)
基本形(1)で定数qだったところが、nの1次式になっているタイプです。
[解法1] 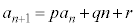 ・・・③ (
・・・③ (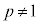 ,
,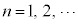 ),
),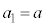 とする。
とする。
③でn→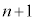 として、
として、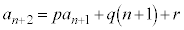 ・・・④ (これを
・・・④ (これを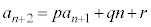 とすると誤りなので要注意)
とすると誤りなので要注意)
④-③により、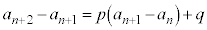
数列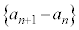 は基本形(1)と同じ形の漸化式に従います。
は基本形(1)と同じ形の漸化式に従います。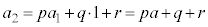 より、
より、
初項は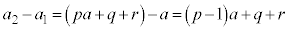
(1)の手順を行えば、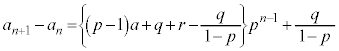
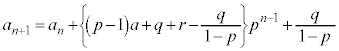 を③に代入すると、
を③に代入すると、
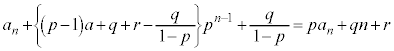
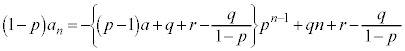
∴ 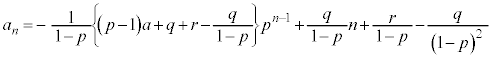
[解法2] 一般項を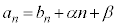 ・・・⑤ とおく。(
・・・⑤ とおく。(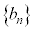 は公比:pの等比数列で、等比数列にnの1次式を加えた形)
は公比:pの等比数列で、等比数列にnの1次式を加えた形)
③に代入して、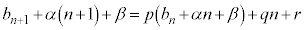
整理すると、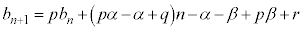
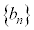 が公比:pの等比数列になるのは、
が公比:pの等比数列になるのは、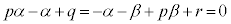 のとき、
のとき、
すなわち、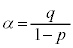 ,
,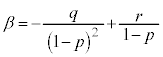
⑤で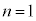 として、
として、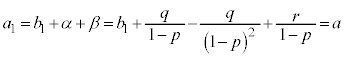
∴ 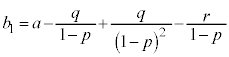
これで、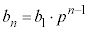 となります。これを⑤に代入して、
となります。これを⑤に代入して、
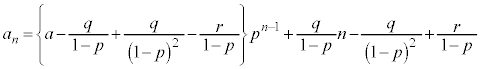
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
数学基礎事項TOP 数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 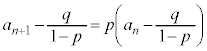
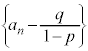 は、初項:
は、初項: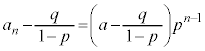
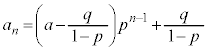
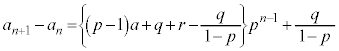
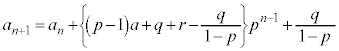 を③に代入すると、
を③に代入すると、