�@���ʃe�X�g���wIIB '23�N��4��@
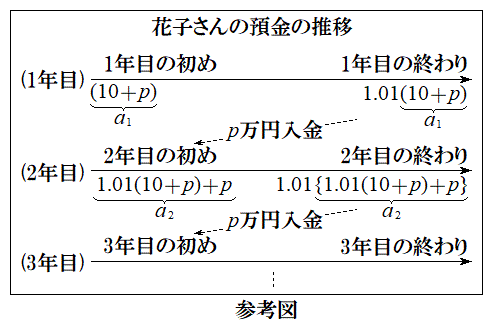 �Ԏq����́A���N�̎n�߂ɗa�������Ɉ��z�̓��������邱�Ƃɂ����B���̓������n�߂�O�ɂ�����Ԏq����̗a����10���~�ł���B�����ŁA�a���Ƃ͗a�������ɂ��邨���̊z�̂��Ƃł���B�a���ɂ͔N��1%�ŗ��������A����N�̏��߂̗a����x���~�ł���A���̔N�̏I���ɂ͗a����
�Ԏq����́A���N�̎n�߂ɗa�������Ɉ��z�̓��������邱�Ƃɂ����B���̓������n�߂�O�ɂ�����Ԏq����̗a����10���~�ł���B�����ŁA�a���Ƃ͗a�������ɂ��邨���̊z�̂��Ƃł���B�a���ɂ͔N��1%�ŗ��������A����N�̏��߂̗a����x���~�ł���A���̔N�̏I���ɂ͗a����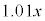 ���~�ƂȂ�B���̔N�̏��߂ɂ�
���~�ƂȂ�B���̔N�̏��߂ɂ�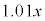 ���~�ɓ����z�����������̂��a���ƂȂ�B
���~�ɓ����z�����������̂��a���ƂȂ�B
���N���߂̓����z��p���~�Ƃ��An�N�ڂ̏��߂̗a����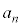 ���~�Ƃ����B�������A
���~�Ƃ����B�������A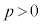 �Ƃ��An�͎��R���Ƃ���B
�Ƃ��An�͎��R���Ƃ���B
�Ⴆ�A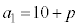 �C
�C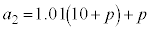 �ł���B
�ł���B
(1) 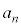 �����߂邽�߂ɓ�̕��j�ōl����B
�����߂邽�߂ɓ�̕��j�ōl����B �|���j�P�|�|�|�|�|�|�|�|�|�|�|�|n�N�ڂ̏��߂̗a����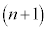 �N�ڂ̏��߂̗a���Ƃ̊W�ɒ��ڂ��čl����B
�N�ڂ̏��߂̗a���Ƃ̊W�ɒ��ڂ��čl����B
�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|3�N�ڂ̏��߂̗a��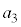 ���~�ɂ��āA
���~�ɂ��āA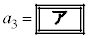 �ł���B���ׂĂ̎��R��n�ɂ���
�ł���B���ׂĂ̎��R��n�ɂ��� �����藧�B�����
�ƕό`�ł��A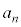 �����߂邱�Ƃ��ł���B
�����߂邱�Ƃ��ł���B
 �̉Q
�̉Q
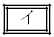 �`
�` �̉Q(�������̂��J��Ԃ��I��ł��悢�B)
�̉Q(�������̂��J��Ԃ��I��ł��悢�B)
 �@
�@ �@�@
�@�@ �@
�@ �@�@
�@�@ �@
�@
 �@p�@�@
�@p�@�@ �@
�@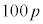 �@�@
�@�@ �@
�@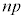
 �@
�@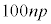 �@�@
�@�@ �@
�@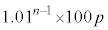 �@�@
�@�@ �@
�@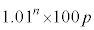
�|���j�Q�|�|�|�|�|�|�|�|�|�|�|�|
���Ƃ��Ɨa�������ɂ�����10���~�Ɩ��N�̏��߂ɓ�������p���~�ɂ��āAn�N�ڂ̏��߂ɂ��ꂼ�ꂪ������ɂȂ邩�ɒ��ڂ��čl����B
�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|
���Ƃ��Ɨa�������ɂ�����10���~�́A2�N�ڂ̏��߂ɂ�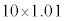 ���~�ɂȂ�A3�N�ڂ̏��߂ɂ�
���~�ɂȂ�A3�N�ڂ̏��߂ɂ�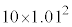 ���~�ɂȂ�B���l�ɍl�����n�N�ڂ̏��߂ɂ�
���~�ɂȂ�B���l�ɍl�����n�N�ڂ̏��߂ɂ�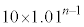 ���~�ɂȂ�B
���~�ɂȂ�B �E1�N�ڂ̏��߂ɓ�������p���~�́An�N�ڂ̏��߂ɂ�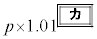 ���~�ɂȂ�B
���~�ɂȂ�B �E2�N�ڂ̏��߂ɓ�������p���~�́An�N�ڂ̏��߂ɂ�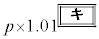 ���~�ɂȂ�B
���~�ɂȂ�B �En�N�ڂ̏��߂ɓ�������p���~�́An�N�ڂ̏��߂ɂ�p���~�̂܂܂ł���B
������
�ƂȂ邱�Ƃ��킩��B�����ŁA �ƂȂ�̂ŁA
�ƂȂ�̂ŁA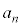 �����߂邱�Ƃ��ł���B
�����߂邱�Ƃ��ł���B
 �C
�C �̉Q(�������̂��J��Ԃ��I��ł��悢�B)
�̉Q(�������̂��J��Ԃ��I��ł��悢�B)  �̉Q
�̉Q �̉Q
�̉Q �@
�@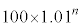 �@�@
�@�@ �@
�@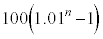
 �@
�@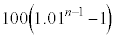 �@�@@3>>�@
�@�@@3>>�@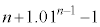
 �@
�@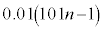 �@�@
�@�@ �@
�@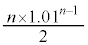
(2) �Ԏq����́A10�N�ڂ̏I���̗a����30���~�ȏ�ɂȂ邽�߂̓����z�ɂ��čl�����B
10�N�ڂ̏I���̗a����30���~�ȏ�ł��邱�Ƃ�s������p���ĕ\����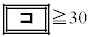 �ƂȂ�B���̕s������p�ɂ��ĉ�����
�ƂȂ�B���̕s������p�ɂ��ĉ����� �ƂȂ�B���������āA���N�̏��߂̓����z���Ⴆ��18000�~�ł���A10�N�ڂ̏I���̗a����30���~�ȏ�ɂȂ邱�Ƃ��킩��B
 �̉Q
�̉Q  �@
�@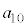 �@�@
�@�@ �@
�@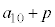 �@�@
�@�@ �@
�@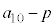
 �@
�@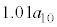 �@�@
�@�@ �@
�@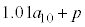 �@�@
�@�@ �@
�@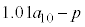
(3) 1�N�ڂ̓������n�߂�O�ɂ�����Ԏq����̗a����10���~�ł͂Ȃ��A13���~�̏ꍇ���l����B���ׂĂ̎��R��n�ɑ��āA���̏ꍇ��n�N�ڂ̏��߂̗a����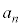 ���~����
���~���� ���~�����B�Ȃ��A�N����1���ł���A���N�̏��߂̓�����p���~�̂܂܂ł���B
���~�����B�Ȃ��A�N����1���ł���A���N�̏��߂̓�����p���~�̂܂܂ł���B  �̉Q
�̉Q �@3�@�@
�@3�@�@ �@13�@�@
�@13�@�@ �@
�@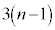
 �@
�@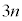 �@�@
�@�@ �@
�@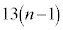 �@�@
�@�@ �@
�@
 �@
�@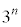 �@�@
�@�@ �@
�@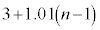 �@�@
�@�@ �@
�@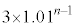
 �@
�@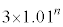 �@�@
�@�@ �@
�@ �@�@
�@�@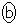 �@
�@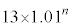
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@���ł͂Ȃ��̂ł����A�v�Z����₱�����A�����͑�ςł��B
(1) 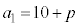 �C
�C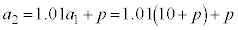
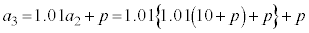 �@�A 2 ......[��]
�@�A 2 ......[��]
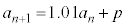 (2���ԑQ�������Q��)�@����@�@�C 0�@�E 3 ......[��]
(2���ԑQ�������Q��)�@����@�@�C 0�@�E 3 ......[��]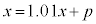 �@����A�@
�@����A�@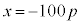
�@�|�A���A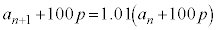 �@�G 4�@�I 0 ......[��]����
�@�G 4�@�I 0 ......[��]����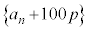 �́A����1.01�C����
�́A����1.01�C����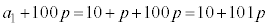 �����䐔���B����āA
�����䐔���B����āA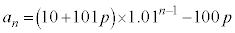 �@����B
�@����B���Ƃ��Ɨa�������ɂ�����10���~�́An�N�ڂ̏��߂ɂ�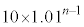 ���~�ɂȂ�܂��B
���~�ɂȂ�܂��B �E1�N�ڂ̏��߂ɓ�������p���~�́An�N�ڂ̏��߂�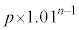 ���~�ɂȂ�܂��B�@�J 2 ......[��]
���~�ɂȂ�܂��B�@�J 2 ......[��] �E2�N�ڂ̏��߂ɓ�������p���~�́An�N�ڂ̏��߂�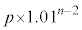 ���~�ɂȂ�܂��B�@�L 3 ......[��]
���~�ɂȂ�܂��B�@�L 3 ......[��] �En�N�ڂ̏��߂ɓ�������p���~�́An�N�ڂ̏��߂�p���~�ł��B
������A
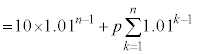 �@�N 2 ......[��]
�@�N 2 ......[��]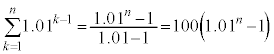 �@�P 1 ......[��]
�@�P 1 ......[��]����������B�����߂��܂��B
(2) 10�N�ڂ̏��߂̗a���͇B��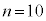 �Ƃ��āA
�Ƃ��āA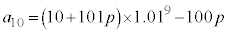
10�N�ڂ̏I���̗a���ɂ��āA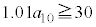 �@�R 3 ......[��]������A
�@�R 3 ......[��]������A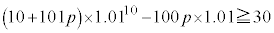
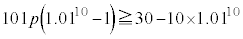 �@��
�@�� 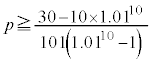 �@�T�V 30�@�X�Z 10 ......[��]
�@�T�V 30�@�X�Z 10 ......[��]���D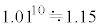 ���A
���A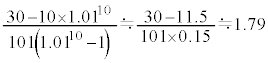 �ł��B
�ł��B
(3) 1�N�ڂ̓����O�̗a����10���~��13���~�ɂȂ�Ƃ��A�B��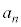 ��
��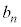 �Ƃ���ƁA
�Ƃ���ƁA 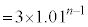 �@�\ 8 ......[��]
�@�\ 8 ......[��](1)�̕��j2�ŁA���Ƃ��Ɨa�������ɂ�����10���~��n�N��̏��߂�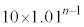 ���~�ɂȂ�A�Ƌ��߂Ă���̂ŁA10���~��13���~�ɂȂ�A
���~�ɂȂ�A�Ƌ��߂Ă���̂ŁA10���~��13���~�ɂȂ�A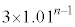 ���~�����Ȃ邱�Ƃ͂����ɂ킩��܂��B
���~�����Ȃ邱�Ƃ͂����ɂ킩��܂��B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 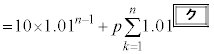
 �ƂȂ�̂ŁA
�ƂȂ�̂ŁA
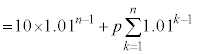 �@�N 2 ......[��]
�@�N 2 ......[��]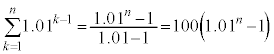 �@�P 1 ......[��]
�@�P 1 ......[��]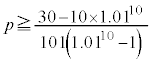 �@�T�V 30�@�X�Z 10 ......[��]
�@�T�V 30�@�X�Z 10 ......[��]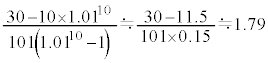 �ł��B
�ł��B