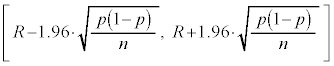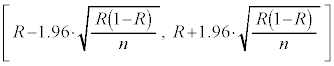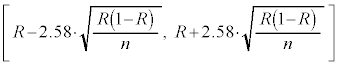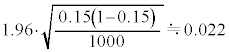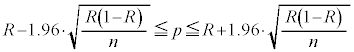�����@�@�@�֘A���
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
��W�c�Ɋւ��������Ă��Ȃ��ŁA�W�{�ׂĕꕽ�ς��䗦�𐄒肵�����Ƃ�������܂��B
�܂��A�ꕽ�ς𐄒肵�܂��B���ɁA�ꕽ�ς�m�C��W������σ���Ƃ��܂��B��W�c����傫��n�̕W�{��ׂɒ��o����ƁAn���[���ɑ傫���Ƃ��A�W�{����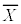 �́A�ߎ��I�ɐ��K���z
�́A�ߎ��I�ɐ��K���z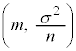 �ɏ]���܂��B
�ɏ]���܂��B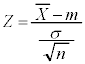 �Ƃ����ƁAZ�͋ߎ��I�ɕW�����K���z
�Ƃ����ƁAZ�͋ߎ��I�ɕW�����K���z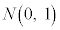 �ɏ]���܂��B(���K���z���Q��)
�ɏ]���܂��B(���K���z���Q��)
��W�c����A�ǂ̂悤�ȗv�f��I��ŕW�{�Ƃ��邩�ɂ���āA�W�{����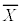 �̒l�͈���Ă��܂����A
�̒l�͈���Ă��܂����A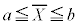 �ƂȂ�m����95%�ƂȂ�
�ƂȂ�m����95%�ƂȂ�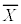 �͈̔͂����߂Ă݂܂��B���ψȏ�ɂȂ�m����
�͈̔͂����߂Ă݂܂��B���ψȏ�ɂȂ�m����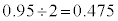 ���A���K���z�\�Œl��0.475�ɂȂ��Ă���Ƃ����T���ƁA
���A���K���z�\�Œl��0.475�ɂȂ��Ă���Ƃ����T���ƁA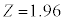 �ł��B
�ł��B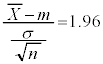 �Ƃ���ƁA
�Ƃ���ƁA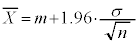 �ƂȂ�܂��B������A���ψȉ��ɂȂ�͈͂��܂߂āA
�ƂȂ�܂��B������A���ψȉ��ɂȂ�͈͂��܂߂āA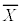 ���A
���A
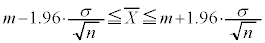 �@����@
�@����@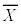 ����ꕽ��m�͈̔͂͂��ꂭ�炢���낤�Ɛ��肷��ƁA�@�����������āAm��
����ꕽ��m�͈̔͂͂��ꂭ�炢���낤�Ɛ��肷��ƁA�@�����������āAm��
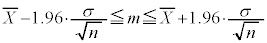 �@����A
�@����A
�ƕ\���܂��Bm���A�͈̔͂ɂ���m����95%�Ƃ����̂ł́A5%�̊m���ŕꕽ�ς̐���l���A�͈̔͊O�ɂȂ邱�Ƃ����蓾��̂ŁA�M���x99%�ɂ������A�Ƃ������Ƃł���A���ψȏ�ƂȂ�m����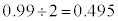 ���A���K���z�\�Œl��0.495�ɂȂ��Ă���Ƃ���T���ƁA
���A���K���z�\�Œl��0.495�ɂȂ��Ă���Ƃ���T���ƁA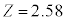 �Ȃ̂ŁA�A�Ɠ��l�ɂ��āA�ꕽ��m�ɑ���M���x99%�̐M����Ԃ́A
�Ȃ̂ŁA�A�Ɠ��l�ɂ��āA�ꕽ��m�ɑ���M���x99%�̐M����Ԃ́A
�ƂȂ�܂��B�A�͈̗̔͂��[�ɂ�σ���܂܂�Ă��܂����A�W�{�������킩���Ă��ĕ�W�c�Ɋւ����Ȃ��Ƃ��Aσ���܂����m�ł��B���̂Ƃ��A�W�{�̑傫��n���[���ɑ傫����A��W����σ�̑���ɁA�W�{�W������p���Ă��悢���Ƃ��m���Ă��܂��B
�ꕽ�ϐ���̐M���x95%�̐M����ԇA�̋�ԕ�w�́A
����́A��W�����ƕW�{�̑傫���݂̂Ō��܂�܂��B�W�{�̗v�f��W�{���ςɂ͈ˑ����܂���B�܂��A�M����Ԃ̕���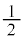 �ɂ��������
�ɂ��������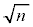 ��2�{�A�܂�W�{�̑傫��n��4�{�ɂ���悢���Ƃ��킩��܂��B
��2�{�A�܂�W�{�̑傫��n��4�{�ɂ���悢���Ƃ��킩��܂��B
��䗦�̐�����l���܂��B�傫��N�̕�W�c�̒��ŁA���鐫��A��L����v�f�̐���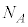 �Ƃ���Ƃ��A
�Ƃ���Ƃ��A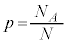 �𐫎�A�̕�䗦�ƌ����܂��B��W�c����傫��n�̕W�{�𒊏o����Ƃ��A����A��L����v�f�̌�X�́A���z
�𐫎�A�̕�䗦�ƌ����܂��B��W�c����傫��n�̕W�{�𒊏o����Ƃ��A����A��L����v�f�̌�X�́A���z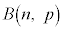 �ɏ]���܂��B�傫��n���[���ɑ傫���Ƃ��A�m���ϐ�X�́A�ߎ��I�ɐ��K���z
�ɏ]���܂��B�傫��n���[���ɑ傫���Ƃ��A�m���ϐ�X�́A�ߎ��I�ɐ��K���z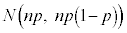 �ɏ]���܂�(���K���z���Q��)�B�܂�A
�ɏ]���܂�(���K���z���Q��)�B�܂�A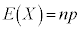 �C
�C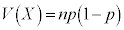 �ł��B�W�{�䗦
�ł��B�W�{�䗦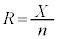 �́A
�́A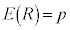 �C
�C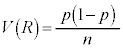 �ƂȂ�(��W�c�ƕW�{���Q��)�̂ŁA���K���z
�ƂȂ�(��W�c�ƕW�{���Q��)�̂ŁA���K���z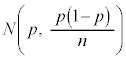 �ɏ]���m���ϐ��ł��B�m���ϐ�
�ɏ]���m���ϐ��ł��B�m���ϐ�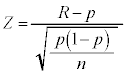 �́A�W�����K���z
�́A�W�����K���z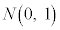 �ɏ]���̂ŁA
�ɏ]���̂ŁA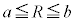 �ƂȂ�m����95%�ƂȂ�R�͈̔͂����߂�ƁA
�ƂȂ�m����95%�ƂȂ�R�͈̔͂����߂�ƁA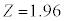 ���A
���A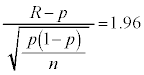 �Ƃ��āA
�Ƃ��āA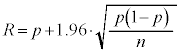 �C������A���ψȉ��ɂȂ�͈͂��܂߂āAR���A
�C������A���ψȉ��ɂȂ�͈͂��܂߂āAR���A
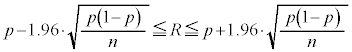 �@����B
�@����B
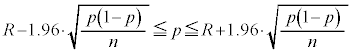 �@����C
�@����C
�ƕ\����܂��B�����ŁA���X���ɂȂ�̂́A���̐M����Ԃ̕\���̒��ɕ���p���܂܂�Ă��邱�ƂŁA�����肵�Ă���͂���p���A���肵�Ă���p�̐M����Ԃ̕\���Ɋ܂߂�͖̂����ł��B���́A�W�{�̑傫��n���[���ɑ傫����A�W�{�䗦�̕��U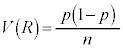 �̒��ɏo�Ă����䗦p��W�{�䗦R�Œu�������Ă��悢���Ƃ��m���Ă��܂��B�������āA�傫��n�̕W�{���琄�肳����䗦��95%�̐M����Ԃ́A
�̒��ɏo�Ă����䗦p��W�{�䗦R�Œu�������Ă��悢���Ƃ��m���Ă��܂��B�������āA�傫��n�̕W�{���琄�肳����䗦��95%�̐M����Ԃ́A
�ƂȂ�܂��B���l�ɁA��䗦�ɑ���99%�̐M����Ԃ́A
��W�c�ƕW�{�̍ŏ��ɏ��������_�����ł����A�W�{�̑傫��1000�l�̐��_�����͗L�����Ƃ������Ƃ��l���Ă݂܂��B
�Ⴆ�A1000�l�ɑ��Ē������s�����Ƃ��A���鐭�}�̎x������15% (1000�l��150�l���x��)���Ƃ��܂��B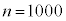 �C
�C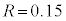 �Ƃ���ƁA
�Ƃ���ƁA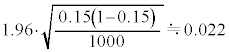
1000�l�̒����ŁA���}�x������95%�̐M����Ԃ́A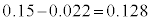 �C
�C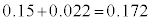 ���A12.8%�ȏ�17.2%�ȉ��Ƃ������ƂɂȂ�܂��B�ꕽ�ς̐���Ɠ��l�ɁA�M����Ԃ̕������߂邽�߂ɂ́A�W�{�̑傫����傫������悭�A�M����Ԃ̕���
���A12.8%�ȏ�17.2%�ȉ��Ƃ������ƂɂȂ�܂��B�ꕽ�ς̐���Ɠ��l�ɁA�M����Ԃ̕������߂邽�߂ɂ́A�W�{�̑傫����傫������悭�A�M����Ԃ̕���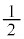 �ɂ��邽�߂ɂ͕W�{�̑傫����4�{�ɂ���悢���Ƃ��킩��܂��B
�ɂ��邽�߂ɂ͕W�{�̑傫����4�{�ɂ���悢���Ƃ��킩��܂��B
��W�c�ɂ����鐭�}�x������15%�̂Ƃ��A1000�l�̕W�{�����ŁA12.8%�ȏ�17.2%�ȉ��̌��ʂł���A���̒����͐M���x95%�ŐM���ł���A�Ƃ�����̂ł����A���ɁA�ʂ̒����ŁA12.8%�����A���邢�́A17.2%���錋�ʂ��o���ꍇ�A15%�Ƃ������}�x�����́A���ł���ƌ��_����܂��B���̂Ƃ��A�u���}�x������15%�ł���v�Ƃ����������A�������ƌ����A�A���������L�Ӑ���5%�����p�����A�Ƃ��������������܂��B12.8%�����A���邢�́A17.2%����͈͂����p���ƌ����܂��B�A�������𐳂����Ƃ���ꍇ�A���p��ɓ��邱�Ƃ͂ق�Ƃ�ǂ��蓾�Ȃ��̂ŁA���p��ɓ����Ă��܂��A�Ƃ����A���蓾�Ȃ����Ƃ��N���Ă��܂��A�Ƃ������Ƃ͌��̉����F�A����������肾�����A�ƍl���܂��B�A�������ɑ��鉼�����Η������ƌ����܂����A�A���������ے肳���Ƃ������Ƃ͑Η������𐳂����A�Ƃ��܂��B
�H�Ɛ��i�̕����܂��A�������̏d���Ȃ�Ƃ������A����Ӗ��ł́A����͋��낵���l�����ł��B�قƂ�ǂ̐l���V������M���Ă���Ƃ��ɒn�������咣���Ă��A�n�����͊��p����Ă��܂��܂��B�I������������f�}����M���ē��[���Ă��܂����ꍇ�ł��A�I���͐����������A�Ƃ���Ă��܂��܂��B����̓������ŁA�����҂����l�łقƂ�ǂ̎����듚�ł������ꍇ�A�듚�������������̕�����肾�A�Ƃ������Ƃɂ���Ă��܂��܂��B�����ҁE��҂��̂Ă�A�Ƃ����C�f�I���M�[�ɂȂ��肩�˂܂���B
��̐��}�x�����ŁA12.8%�ȉ������A���邢�́A17.2%���������p��Ƃ���ꍇ���Б������A���������p��Ƃ���ꍇ�����������ƌ����܂��B
��W����σ�̕�W�c����傫��n�̕W�{�𒊏o���ĕW�{���ς�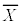 �Ƃ���ƁAn���[���ɑ傫����A�ꕽ��m�ɑ���95%�̐M����Ԃ�(��W����σ�́A�W�{���ς̕W����
�Ƃ���ƁAn���[���ɑ傫����A�ꕽ��m�ɑ���95%�̐M����Ԃ�(��W����σ�́A�W�{���ς̕W����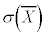 �Œu�������Ă��悢)�A
�Œu�������Ă��悢)�A
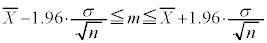
��W�c����傫��n�̕W�{�𒊏o���āA�W�{�䗦��R�Ƃ���ƁA��䗦p�ɑ���95%�̐M����Ԃ́A
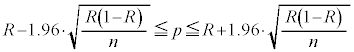
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���w��b����TOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2025(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 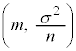 �ɏ]���܂��B
�ɏ]���܂��B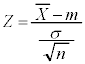 �Ƃ����ƁA
�Ƃ����ƁA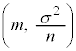 �ɏ]���܂��B
�ɏ]���܂��B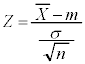 �Ƃ����ƁAZ�͋ߎ��I�ɕW�����K���z
�Ƃ����ƁAZ�͋ߎ��I�ɕW�����K���z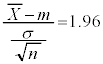 �Ƃ���ƁA
�Ƃ���ƁA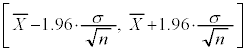
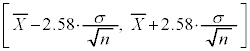
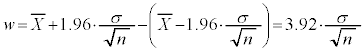
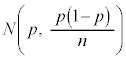 �ɏ]���m���ϐ��ł��B�m���ϐ�
�ɏ]���m���ϐ��ł��B�m���ϐ�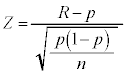 �́A�W�����K���z
�́A�W�����K���z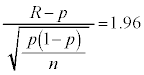 �Ƃ��āA
�Ƃ��āA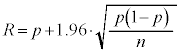 �C������A���ψȉ��ɂȂ�͈͂��܂߂āAR���A
�C������A���ψȉ��ɂȂ�͈͂��܂߂āAR���A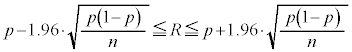 �@����B
�@����B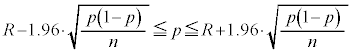 �@����C
�@����C