�w���@���̊g���@�@�@�֘A���
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
m�Cn�����R���Aa�������Ƃ��āA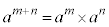 �C
�C ���������܂�(�w���@���Q��)�B
���������܂�(�w���@���Q��)�B
�w���@���F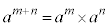 �ɂ����āA
�ɂ����āA �Ƃ��Ă݂�ƁA
�Ƃ��Ă݂�ƁA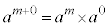 �ƂȂ�܂����A
�ƂȂ�܂����A �𐬂藧�����邽�߂ɂ́A
�𐬂藧�����邽�߂ɂ́A �Ƃ���悢���Ƃ��킩��܂��B
�Ƃ���悢���Ƃ��킩��܂��B
n�̐����Ƃ��āA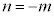 �Ƃ���ƁA
�Ƃ���ƁA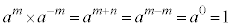 �ƂȂ�̂ŁA
�ƂȂ�̂ŁA �ƍl����悢���Ƃ��킩��܂��B
�ƍl����悢���Ƃ��킩��܂��B
l�Cm�����R���Ƃ��āA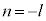 �Ƃ��܂��B
�Ƃ��܂��B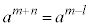
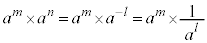
�����ŁA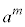 ��a��m�������́A
��a��m�������́A ��a��l�������̂Ȃ̂ŁA
��a��l�������̂Ȃ̂ŁA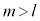 �Ȃ�A
�Ȃ�A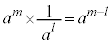 �C
�C �Ȃ�A
�Ȃ�A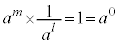 �C
�C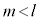 �Ȃ�A
�Ȃ�A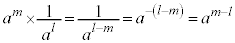 �ł���A������ɂ��Ă��Am�𐳂̐����An�̕��̐����Ƃ��Ă��A
�ł���A������ɂ��Ă��Am�𐳂̐����An�̕��̐����Ƃ��Ă��A �����藧���܂��B
�����藧���܂��B
m�����̐����An�����̐����̏ꍇ�ɂ��A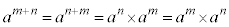
m�Cn���Ƃ��ɕ��̐����ŁAk�Cl�𐳂̐����Ƃ��āA �C
�C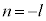 �̂Ƃ����A
�̂Ƃ����A
�܂��Al�Cm�𐳂̐����An�̐����� ���Ƃ��āA
���Ƃ��āA
l�Cn�𐳂̐����Am�̐�����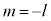 ���Ƃ��āA
���Ƃ��āA
m�Cn���Ƃ��ɕ��̐����ŁAk�Cl�𐳂̐������Ƃ��āA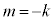 �C
�C �̂Ƃ����A
�̂Ƃ����A
m�Cn�̂����ꂩ�����0�A���邢�́A�Ƃ���0�̏ꍇ�ɂ��A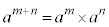 �C
�C �����藧���܂��B
�����藧���܂��B
�ȏ���A�w���@���F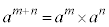 �C
�C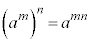 �́Am�Cn�������̏ꍇ�ɂ���(���̐����ł����Ă��A0�ł����Ă��悢)���藧���܂��B
�́Am�Cn�������̏ꍇ�ɂ���(���̐����ł����Ă��A0�ł����Ă��悢)���藧���܂��B
�ȉ��A ���Ƃ��܂��B
���Ƃ��܂��B
�w���@���F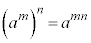 �ɂ����āAm���L�����ł���Ƃ��āA
�ɂ����āAm���L�����ł���Ƃ��āA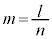 (l�͐����An�͎��R��)�Ƃ��Ă݂܂��B
(l�͐����An�͎��R��)�Ƃ��Ă݂܂��B
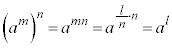 �𐬂藧�����邽�߂ɂ́A
�𐬂藧�����邽�߂ɂ́A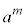 ��n�悪
��n�悪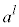 �Ȃ̂ŁA
�Ȃ̂ŁA ��
��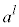 ��n�捪�ł���悢���ƂɂȂ�܂��B
��n�捪�ł���悢���ƂɂȂ�܂��B
���̂Ƃ��A ���A
���A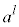 ��n�捪�ŁAn�������̏ꍇ�ɂ͐��̕����Ƃ��āA
��n�捪�ŁAn�������̏ꍇ�ɂ͐��̕����Ƃ��āA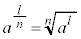 ���Ɩ��܂�(�ݏ捪���Q��)�B
���Ɩ��܂�(�ݏ捪���Q��)�B
�w�����L�����ɂȂ�ꍇ�A�L�������ŕ\���āA(�L����)��́A(���q)���(����)�捪�A�Ƃ������ƂɂȂ�܂��B
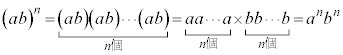 �����藧�̂ŁA
�����藧�̂ŁA
n�����R���Al�Cm�𐮐����Ƃ��āA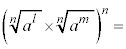
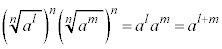
�]���āA �́A
�́A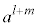 ��n�捪�ŁA
��n�捪�ŁA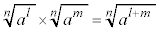 �@����@ �����藧���܂��B
�@����@ �����藧���܂��B
q�Cs�����R���Ap�Cr�𐮐����Ƃ��āA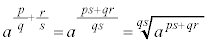
�@���A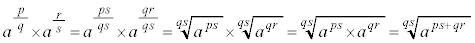
�� 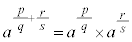 �@����A
�@����A
m�����R���Al�Cn�𐮐����Ƃ��āA ��
��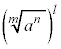 �́A�Ƃ���m�悵�Ă݂�ƁA
�́A�Ƃ���m�悵�Ă݂�ƁA
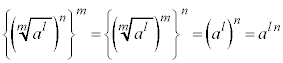
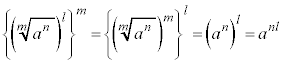
��  �@����B �����藧���܂��B
�@����B �����藧���܂��B
m�Cn�����R�����Ƃ��āA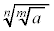 ��
��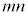 �悷��ƁA
�悷��ƁA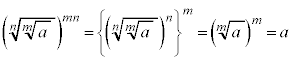 �ƂȂ�̂ŁAa��
�ƂȂ�̂ŁAa��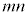 �捪�ł��B�܂�A
�捪�ł��B�܂�A
 �@����C �����藧���܂��B
�@����C �����藧���܂��B
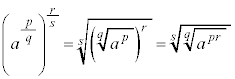 (�� �B)
(�� �B)
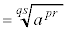 (�� �C)
(�� �C)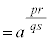 �@����D
�@����D �C
�C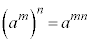 �́Am�Cn���L�����̏ꍇ�ɂ��������܂��B
�́Am�Cn���L�����̏ꍇ�ɂ��������܂��B
���́A�w���@���́A�w���������A�����̏ꍇ�ɂ��������邱�Ƃ��킩���Ă��܂��B
�w�����~����π�̂悤�Ȗ������̏ꍇ�A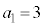 �C
�C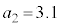 �C
�C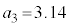 �C
�C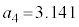 �C
�C �C����C�̂悤�ɁA�e�����L�����ł����āA
�C����C�̂悤�ɁA�e�����L�����ł����āA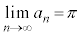 �ƂȂ�悤�Ȑ���
�ƂȂ�悤�Ȑ���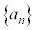 ���l���A���̐�b�ɑ��āA
���l���A���̐�b�ɑ��āA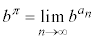 �Ƃ��āA
�Ƃ��āA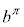 ���l���܂��B
���l���܂��B
�w����π�ȊO�̖�����a�̏ꍇ�����l�ɂ��āA���̐�b�ɑ��āA ���l���܂��B
���l���܂��B
�w���@���F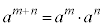 �C
�C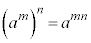 �@(
�@( �Cm�Cn�͎���)
�Cm�Cn�͎���)
�ȏ�ɂ��A���R���Ɍ����Ă����w���������S�̂Ɋg�����邱�Ƃɂ��܂��B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���w��b����TOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 


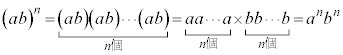 �����藧�̂ŁA
�����藧�̂ŁA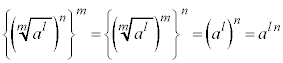
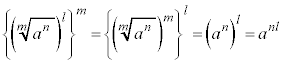
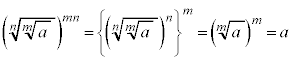 �ƂȂ�̂ŁAa��
�ƂȂ�̂ŁAa��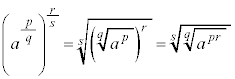 (�� �B)
(�� �B)