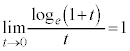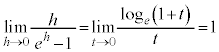�Ɍ��̌����@�@�@�֘A���
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
(1) 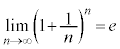 �@(e�F���R�ΐ��̒�A
�@(e�F���R�ΐ��̒�A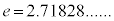 )
)
(2) 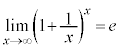
(3) 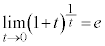
(4) 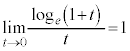
(5) 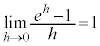
(6) 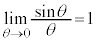
[�ؖ�](1) ����́A���̃E�F�u�E�T�C�g�ł́Ae�̒�`�Ƃ������Ƃɂ��Ă����܂��B
�藝���A
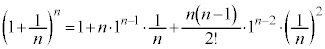
�@�@�@�@�@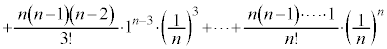
�@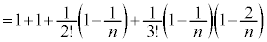
�@�@�@�@�@�@�@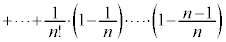
�@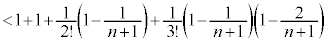
�@�@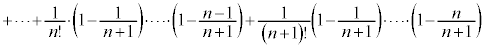
(�Ō�ɐ��̒l������1���������Ă��邱�Ƃɒ���)
�@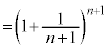
�]���āA����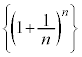 �͒P�������Ȑ���B�@����@
�͒P�������Ȑ���B�@����@
�܂��A
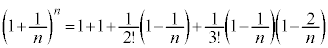
�@�@�@�@�@�@�@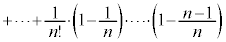
�@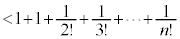
�@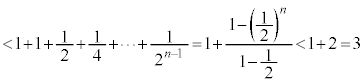
�]���āA����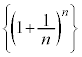 �͏�ɗL�E(���E������Ƃ����Ӗ��ł�)�Ȑ���B�@����A
�͏�ɗL�E(���E������Ƃ����Ӗ��ł�)�Ȑ���B�@����A
�@�C�A���A�P�����L�E�Ȑ���͋Ɍ��l�����Ƃ����藝(���Z�͈̔͊O�ł�)�ɂ��A����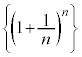 �́A
�́A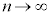 �̂Ƃ��������ċɌ��l�������܂��B
�̂Ƃ��������ċɌ��l�������܂��B
���̋Ɍ��l�����R�ΐ��̒�e�ƒ�`���܂��B�����A
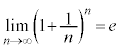
e�́A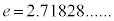 �ŁA�������ł��邱�Ƃ��m���Ă��܂��B
�ŁA�������ł��邱�Ƃ��m���Ă��܂��B
(2) 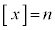 �Ƃ��āA
�Ƃ��āA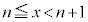 ���A
���A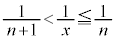
�e�ӂ�1��������n�悵�Ă��s�����̌����͕ς��܂���B
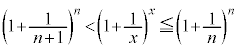
�����ŁA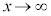 �Ƃ���ƁA
�Ƃ���ƁA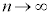 �ł����āA�E�ӂ́A
�ł����āA�E�ӂ́A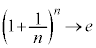
���ӂ́A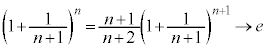
����āA�͂��݂����̌������A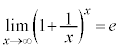
(3) (2)�ɂ����āA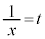 �Ƃ��ƁA
�Ƃ��ƁA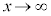 �̂Ƃ��A
�̂Ƃ��A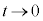
����āA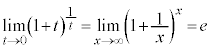
(4) (3)�ɂ����āA���R�ΐ�(e���Ƃ���ΐ�)���l���܂��B
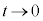 �̂Ƃ��A
�̂Ƃ��A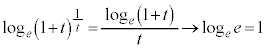
�� 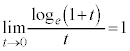
(5) (4)�ɂ����āA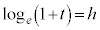 �Ƃ����ƁA
�Ƃ����ƁA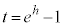
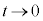 �̂Ƃ��A
�̂Ƃ��A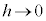
����āA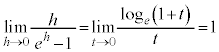
�� 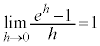
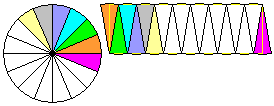 (6) ���a1�̉~���̒�����
(6) ���a1�̉~���̒�����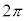 �ƒ�`����Ă��܂��B
�ƒ�`����Ă��܂��B
�E�}�̂悤�ɁA�~��n����������`���㉺�݂��Ⴂ�ɕ��ׂ��}�`���l���܂��B
���̐}�`�́A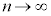 �Ƃ���ƁA�c��1�C�����~���̒�����
�Ƃ���ƁA�c��1�C�����~���̒�����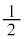 (�~���̒������㉺�ɕ�����邩��)�C����π?�̒����`(�ʐς�π )�ɋ߂Â��Ă����܂��B
(�~���̒������㉺�ɕ�����邩��)�C����π?�̒����`(�ʐς�π )�ɋ߂Â��Ă����܂��B
���̐}�`�͂��Ƃ��Ɖ~�������̂ŁA���a1�̉~�̖ʐς�π �Ƃ������ƂɂȂ�܂��B
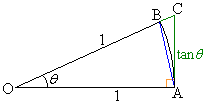 ���x�́A�E�}�̂悤�Ȓ��pθ �̐�`OAB���l���܂��B���炩�ɁA
���x�́A�E�}�̂悤�Ȓ��pθ �̐�`OAB���l���܂��B���炩�ɁA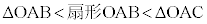 �ł��B
�ł��B
��`OAB�̖ʐς́A���a1�̉~�̖ʐς�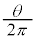 �{�ŁA
�{�ŁA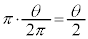 �ł��B
�ł��B
����āA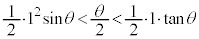
2�������āA�e�ӂ̋t�����l����ƁA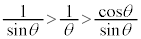
�� 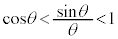
�����ŁA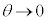 �Ƃ���ƁA���ӂ́A
�Ƃ���ƁA���ӂ́A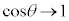
����āA�͂��݂����̌������A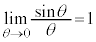
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���w��b����TOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 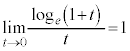
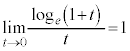
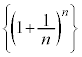 �͒P�������Ȑ���B�@����@
�͒P�������Ȑ���B�@����@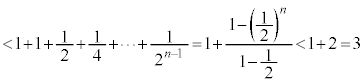
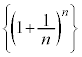 �͏�ɗL�E(���E������Ƃ����Ӗ��ł�)�Ȑ���B�@����A
�͏�ɗL�E(���E������Ƃ����Ӗ��ł�)�Ȑ���B�@����A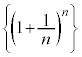 �́A
�́A