�����嗝�H���w'08�N[3]
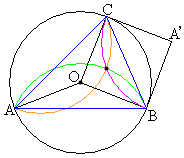 �s�p�O�p�`ABC�̊O�ډ~S�̒��S(�O�S)��O�Ƃ��AS�̔��a��R�Ƃ���B�~S�̌�
�s�p�O�p�`ABC�̊O�ډ~S�̒��S(�O�S)��O�Ƃ��AS�̔��a��R�Ƃ���B�~S�̌�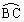 �C
�C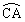 �C
�C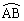 �ƒ���BC�CCA�CAB�Ɋւ��đΏ̂ȉ~�ʂ����ꂼ��
�ƒ���BC�CCA�CAB�Ɋւ��đΏ̂ȉ~�ʂ����ꂼ��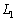 �C
�C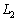 �C
�C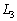 �Ƃ���B���̂Ƃ��A3�̌�
�Ƃ���B���̂Ƃ��A3�̌�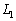 �C
�C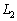 �C
�C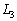 �͎O�p�`ABC�̐��S�Ō����B���̂��Ƃ����̂悤�ɂ��Ď����B
�͎O�p�`ABC�̐��S�Ō����B���̂��Ƃ����̂悤�ɂ��Ď����B
�O�p�`ABC�̊O�SO�ƒ���BC�CCA�CAB�Ɋւ��đΏ̂ȓ_�����ꂼ��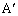 �C
�C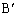 �C
�C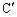 �Ƃ���B�܂��A
�Ƃ���B�܂��A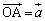 �C
�C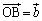 �C
�C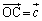 �Ƃ��AH��
�Ƃ��AH��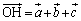 �ɂ���܂�_�Ƃ���B
�ɂ���܂�_�Ƃ���B
(1) 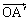 �C
�C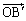 �C
�C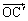 ��
��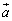 �C
�C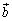 �C
�C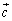 ��p���ĕ\���B
��p���ĕ\���B (2) 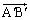 ��
��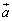 ��
��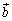 �ŕ\���A�O�p�`
�ŕ\���A�O�p�`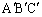 �͎O�p�`ABC�ƍ����ł��邱�Ƃ������B
�͎O�p�`ABC�ƍ����ł��邱�Ƃ������B (3) 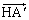 �C
�C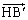 �C
�C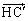 ��
��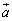 �C
�C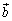 �C
�C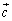 ��p���ĕ\���A3�̌�
��p���ĕ\���A3�̌�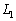 �C
�C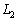 �C
�C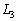 �͓_H�Ō���邱�Ƃ������B
�͓_H�Ō���邱�Ƃ������B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@�U�����Ȃ���Γ��ł����A�e�ȗU�������Ă���̂Ōy���ɉ����Ă䂯��Ǝv���܂��B
(1) ��BC�CCA�CAB�̒��_��K�CM�CN�Ƃ��܂��B
O��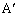 ��BC�Ɋւ��đΏ́CO��
��BC�Ɋւ��đΏ́CO��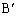 ��CA�Ɋւ��đΏ́CO��
��CA�Ɋւ��đΏ́CO��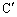 ��AB�Ɋւ��đΏ̂Ȃ̂ŁA
��AB�Ɋւ��đΏ̂Ȃ̂ŁA
(2) 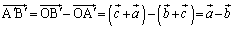 ......[��]
......[��] ������A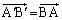 �ł��B���l�ɁA
�ł��B���l�ɁA ����āA�O�p�`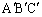 �ƎO�p�`ABC�́A3�ӂ��������A�����ł��B
�ƎO�p�`ABC�́A3�ӂ��������A�����ł��B
(3) 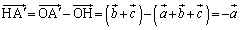
����āA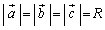 ���A
���A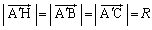 �ł��B
�ł��B
�Ƃ������Ƃ́AH�CB�CC��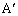 �𒆐S�Ƃ��锼�aR�̉~����̓_�ł���AH�́A�~��
�𒆐S�Ƃ��锼�aR�̉~����̓_�ł���AH�́A�~��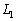 ��̓_�ł��B����@
��̓_�ł��B����@
���l�ɂ��āA ����āA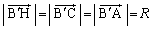 �ł����āAH�CC�CA��
�ł����āAH�CC�CA��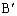 �𒆐S�Ƃ��锼�aR�̉~����̓_�ł���AH�́A�~��
�𒆐S�Ƃ��锼�aR�̉~����̓_�ł���AH�́A�~��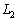 ��̓_�ł��B����A
��̓_�ł��B����A ����āA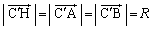 �ł����āAH�CA�CB��
�ł����āAH�CA�CB��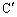 �𒆐S�Ƃ��锼�aR�̉~����̓_�ł���AH�́A�~��
�𒆐S�Ƃ��锼�aR�̉~����̓_�ł���AH�́A�~��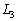 ��̓_�ł��B����B
��̓_�ł��B����B
�O�p�`ABC�͉s�p�O�p�`�Ȃ̂ŁA�@�C�A�C�B���A3�̌�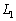 �C
�C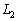 �C
�C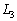 �͓_H�Ō����܂��B
�͓_H�Ō����܂��B
(4) 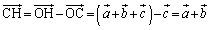 ......[��]
......[��] �� 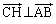
�� 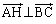
�� 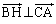 �ȏ���AH�͎O�p�`ABC�̐��S�ł��B
�ȏ���AH�͎O�p�`ABC�̐��S�ł��B
�NjL�D�悭�m��ꂽ�����ł����A�O�S�Ɍ��_������Ƃ��āA�O�p�`ABC�̏d�SG�̈ʒu�x�N�g���́A
�ƂȂ�A���SH�̈ʒu�x�N�g�����A
�ł���Ƃ������Ƃ́A�d�SG�́A�O�SO�Ɛ��SH�����Ԑ���OH��1�F2�ɓ�������_���Ƃ������Ƃł��B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B