�Q�n��㐔�w'08�N[5]
���̖₢�ɓ�����B
(1) α�������Ƃ��A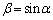 �C
�C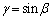 �Ƃ����B���̂Ƃ��A
�Ƃ����B���̂Ƃ��A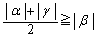 ���ؖ�����B
���ؖ�����B (2) 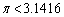 ��p���āA
��p���āA �������B
�������B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@(1) �ؖ����ׂ����̍��ӂ��A ��
�� �̑������ςƌ��Ă����������̂����肻���ł��B�����ŁA�ؖ����ׂ�����ό`���܂��B
�̑������ςƌ��Ă����������̂����肻���ł��B�����ŁA�ؖ����ׂ�����ό`���܂��B ����ɁA ��
�� 1���ڍ����āA
1���ڍ����āA ���������ό`�͂悭�s������̂ł��B
���āA�����ŁA �C
�C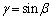 ��������ƁA
��������ƁA �ƂȂ��āA���ӂƉE�ӂ������`�ɂȂ�܂��B��ӂ́A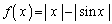 �Ƃ���Ƃ��A
�Ƃ���Ƃ��A  �@����@
�@����@���ؖ�����ƌ����Ă��邱�Ƃ��킩��܂��B
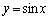 ��
��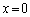 �ɂ������ڐ���
�ɂ������ڐ���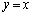 �ŁA
�ŁA �ł��邱�Ƃ��v�������ׂ܂��傤�B
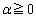 �ł���
�ł��� �ƂȂ�悤��α�C�Ⴆ�A
�ƂȂ�悤��α�C�Ⴆ�A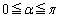 ����α�������Ă��܂��B
����α�������Ă��܂��B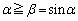 �Ȃ̂ŁA
�Ȃ̂ŁA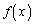 ���P�������ł��邱�Ƃ�������A�@�������܂��Bα�����ׂĂ̎����ōl�����
���P�������ł��邱�Ƃ�������A�@�������܂��Bα�����ׂĂ̎����ōl����� �̕������R���R���ς��̂Ŗʓ|�ł��B�����ŁA
�̕������R���R���ς��̂Ŗʓ|�ł��B�����ŁA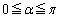 �̏ꍇ�Ƃ���ȊO�̏ꍇ���čl���邱�Ƃɂ��܂��B
�̏ꍇ�Ƃ���ȊO�̏ꍇ���čl���邱�Ƃɂ��܂��B
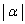 ���傫���Ȃ�ƁA
���傫���Ȃ�ƁA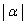 ��
�� (
(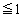 )�Ƃ̍����傫���Ȃ��āA�s�����������₷���Ȃ�͂��ł��B
)�Ƃ̍����傫���Ȃ��āA�s�����������₷���Ȃ�͂��ł��B
(i) 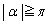 �̂Ƃ��A
�̂Ƃ��A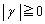 ���A
���A �܂��A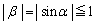
����āA �@����A
�@����A (ii) 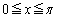 �ɂ����āA��
�ɂ����āA��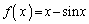 ���l���܂��B
���l���܂��B ���A �́A
�́A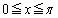 �ɂ����ĒP�������Ȋ��ł��B
�ɂ����ĒP�������Ȋ��ł��B
����āA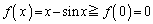
�� 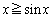 �]���āA
�]���āA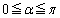 �ł���A
�ł���A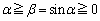 �ł��B
�ł��B
 ���P�������ł��邱�Ƃ���A
���P�������ł��邱�Ƃ���A
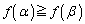
�܂�A  �@����B
�@����B���������܂��B
 �̂Ƃ��A
�̂Ƃ��A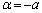 �C
�C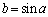 �Ƃ��āA
�Ƃ��āA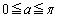 �C�B���A
�C�B���A �� 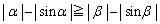
����āA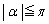 �̂Ƃ��A
�̂Ƃ��A �� 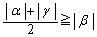 �@(������
�@(������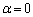 �̂Ƃ�)
�̂Ƃ�) (i)�C(ii)���A���ׂĂ̎���α�ɂ��āA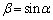 �C
�C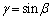 �Ƃ����Ƃ��A
�Ƃ����Ƃ��A 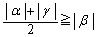 �@(������
�@(������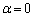 �̂Ƃ�)
�̂Ƃ�)(�ؖ��I)
(2)  �����鐔�l���傫�����Ƃ����������̂ŁA(1)�̕s�����̍��ӂ�
�����鐔�l���傫�����Ƃ����������̂ŁA(1)�̕s�����̍��ӂ�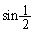 ���o�Ă���悤�ɂ��āA
���o�Ă���悤�ɂ��āA �� 
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B