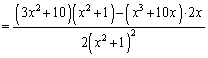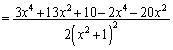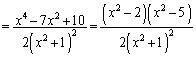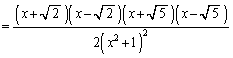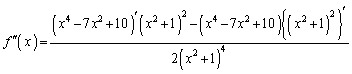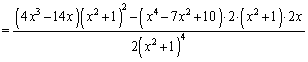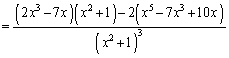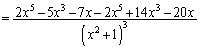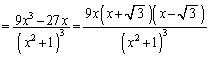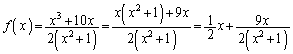北見工大数学'08年[5]
一般に、直線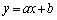
が関数
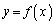のグラフの漸近線であるとは、
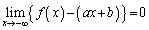または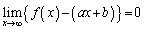 
であることを言う。
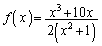とするとき、以下の問いに答えよ。
(1) 
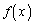の増減を調べ、
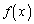が極小になるxの値、
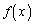が極大になるxの値があればそれぞれすべて求めよ。 (2) 
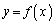が下に凸になるxの範囲を求めよ。 (3) 
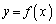に変曲点があればすべて求め、それぞれの点における
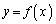の接線の傾きを求めよ。 (4) 
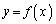の漸近線をすべて求めよ。 (5) 
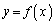のグラフの概形を描け。また、(3)で求めた変曲点があればそれぞれの変曲点における接線を、(4)で求めた漸近線があれば漸近線を、
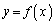のグラフと同じxy平面上に描け。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
解答 漸近線や変曲点は入試ではあまり見かけないテーマですが、この問題でしっかり確認しておいてください。
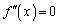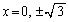
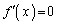とすると、
とすると、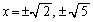
，
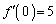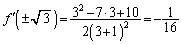
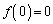
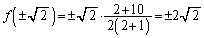(複号同順)
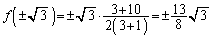(複号同順)
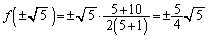(複号同順)
| x |
|  |
|  |
|  |
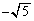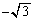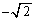| 0 |
|  |
|  |
|  |
|
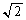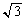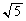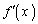 | ＋ | 0 | − | − | − | 0 | ＋ | ＋ | ＋ | 0 | ― | ― | ― | 0 | ＋ |
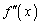 | ― | ― | ― | 0 | ＋ | ＋ | ＋ | 0 | ― | ― | ― | 0 | ＋ | ＋ | ＋ |
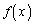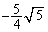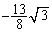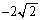 |  |  |  |  |  |  |  | 0 | |  | |  | |  | |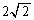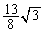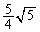
(1) 
の増減は上記増減表の通り。増減表より、
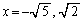のとき極大、
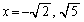のとき極小 ......[答] (2) 増減表より、下に凸の範囲は、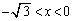
，
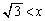......[答] (3) 増減表より、変曲点は、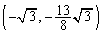
(接線の傾き：
)，
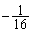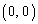(接線の傾き：5)，
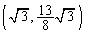(接線の傾き
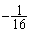) ......[答] (4) 
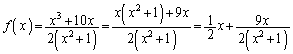
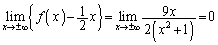より、漸近線は、
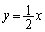......[答]
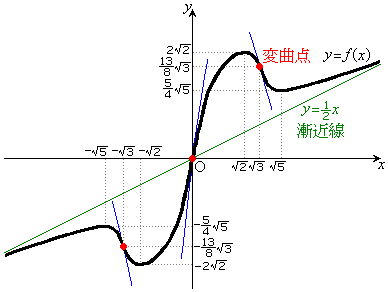(5) 右図で、
のグラフが太線、変曲点は赤マル、接線は青線、漸近線は緑線。右図は誇張して描かれていますが、実際には、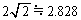
，
，
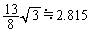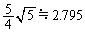で、極値の絶対値はほぼ同じ値です。
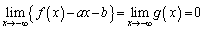あるいは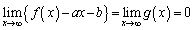 
より、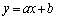
が漸近線である、としておけばよいでしょう。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中！理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 
と表せるような
で、
または 
のときは、
