�����H���w'08�N[3]
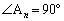 �C
�C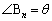 �ł��鑊���Ȓ��p�O�p�`
�ł��鑊���Ȓ��p�O�p�`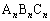 (
(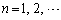 )���A���̂悤�ȋK���ō��W���ʏ�ɕ��ׂ��Ă���B
)���A���̂悤�ȋK���ō��W���ʏ�ɕ��ׂ��Ă���B
�K��1) �O�p�`�ǂ������A�ӈȊO�ŏd�Ȃ邱�Ƃ͂Ȃ��B
�K��2) ���_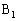 �͍��W���ʏ�̌��_
�͍��W���ʏ�̌��_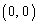 �ƈ�v���A
�ƈ�v���A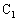 �͓_
�͓_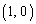 �ƈ�v���Ă���B�܂��A
�ƈ�v���Ă���B�܂��A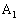 �͑�1�ی��ɂ���B
�͑�1�ی��ɂ���B �K��3) m�����R���Ƃ���Ƃ��A�O�p�`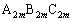 �ƎO�p�`
�ƎO�p�`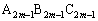 �ɂ����āA
�ɂ����āA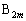 ��
��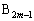 �ƈ�v���A
�ƈ�v���A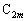 ��
��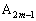 �ƈ�v���Ă���B
�ƈ�v���Ă���B ����ɁA�O�p�`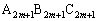 �ƎO�p�`
�ƎO�p�`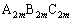 �ɂ����āA���_
�ɂ����āA���_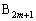 ��
��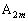 �ƈ�v���A
�ƈ�v���A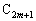 ��
��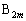 �ƈ�v���Ă���B
�ƈ�v���Ă���B ���̖₢�ɓ�����B
(1) 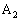 �̍��W���Aθ ��p���ĕ\���B
�̍��W���Aθ ��p���ĕ\���B (2) 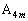 (
(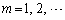 )�̍��W
)�̍��W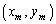 ���Aθ ��p���ĕ\���B
���Aθ ��p���ĕ\���B (3) 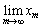 �����
�����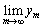 �����߂�B
�����߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
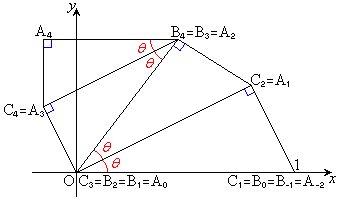 ���@��₱�����ł��Ă�����Ȃ̂ŁA���J�ɋK������T���Ă����܂��B�K��1)�`3)�ɉ����ĎO�p�`
���@��₱�����ł��Ă�����Ȃ̂ŁA���J�ɋK������T���Ă����܂��B�K��1)�`3)�ɉ����ĎO�p�`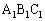 �C�O�p�`
�C�O�p�`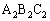 �C�O�p�`
�C�O�p�`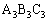 �C�O�p�`
�C�O�p�`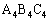 ��}�����Ă����ƁA�E�}�̂悤�ɂȂ�܂��B�Ƃ肠�����A(1)��
��}�����Ă����ƁA�E�}�̂悤�ɂȂ�܂��B�Ƃ肠�����A(1)��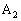 �̍��W�����߂܂����A(2)�ł�
�̍��W�����߂܂����A(2)�ł�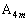 ���Ă���̂ŁA
���Ă���̂ŁA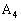 �C
�C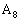 �C
�C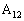 ���ǂ�ȋK���ɕ��Ԃ̂����l���邱�ƂɂȂ�܂��B
���ǂ�ȋK���ɕ��Ԃ̂����l���邱�ƂɂȂ�܂��B
�K��3)���A�O�p�`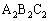 �ƎO�p�`
�ƎO�p�`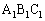 �ɂ����āA
�ɂ����āA
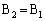 �C
�C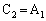
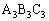 �ƎO�p�`
�ƎO�p�`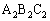 �ɂ����āA
�ɂ����āA
�O�p�`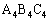 �ƎO�p�`
�ƎO�p�`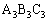 �ɂ����āA
�ɂ����āA
������A
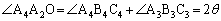 �C
�C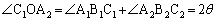
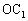 //
// 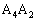
���l�ɁA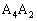 //
// 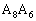
�ȂǂƂȂ��Ă����ł��傤�B�܂��A
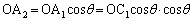 �C
�C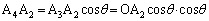
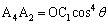 �ƂȂ��Ă��܂��B���l�ɂ���A
�ƂȂ��Ă��܂��B���l�ɂ���A
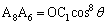 �C
�C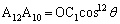
�K������������x�����Ă�����A���Ăł́A�K�����������Ƃ��낾�������グ��悤�ɂ��܂��B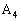 �C
�C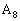 �C��� �ƒ��ׂčs���Ă��悢�̂ł����A
�C��� �ƒ��ׂčs���Ă��悢�̂ł����A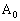 �C
�C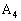 �C��� �Ƃ�����������₷���̂ŁA�K��1)�`3)�ɉ����āA�O�p�`
�C��� �Ƃ�����������₷���̂ŁA�K��1)�`3)�ɉ����āA�O�p�`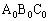 �̕��ւ����̂ڂ邱�Ƃɂ��܂��B�܂��A�O�p�`
�̕��ւ����̂ڂ邱�Ƃɂ��܂��B�܂��A�O�p�`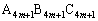 �`�O�p�`
�`�O�p�`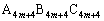 ���l���܂��B���Ă��܂Ƃ߂�Ƃ��ɂ́A�x�N�g�����g���̂��悢�Ǝv���܂��B
���l���܂��B���Ă��܂Ƃ߂�Ƃ��ɂ́A�x�N�g�����g���̂��悢�Ǝv���܂��B
(1) �E��̐}���A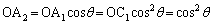 �@(
�@(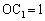 )
) 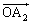 �́Ax���������琳������
�́Ax���������琳������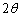 ����������������x�N�g���Ȃ̂ŁA
����������������x�N�g���Ȃ̂ŁA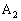 �̍��W�́A
�̍��W�́A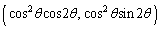 ......[��]
......[��]
(2) ��ӂ́A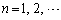 �Ƃ��Ē��p�O�p�`
�Ƃ��Ē��p�O�p�`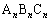 ���`���Ă���̂ł����A�K��1)�`3)��p���āA���p�O�p�`
���`���Ă���̂ł����A�K��1)�`3)��p���āA���p�O�p�`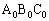 �C���p�O�p�`
�C���p�O�p�`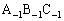 �C��� ���l����ƁA�K��3)��
�C��� ���l����ƁA�K��3)��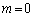 �Ƃ��āA
�Ƃ��āA �ƂȂ邱�Ƃ��킩��܂��B
������A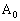 �͌��_O�Ɉ�v���A
�͌��_O�Ɉ�v���A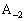 ��
��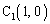 �Ɉ�v���܂��B
�Ɉ�v���܂��B 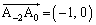 �@����@
�@����@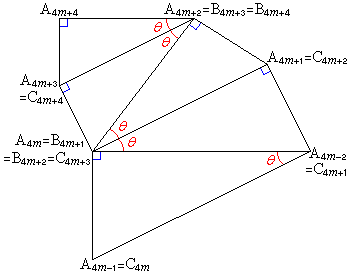 �_
�_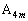 �Ɠ_
�Ɠ_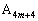 �̊W�ׂ邽�߂ɁA�E�}(�O�p�`
�̊W�ׂ邽�߂ɁA�E�}(�O�p�`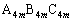 �`�O�p�`
�`�O�p�`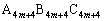 )���l���܂��B�K��3)���Am��0�ȏ�̐����Ƃ��āA
)���l���܂��B�K��3)���Am��0�ȏ�̐����Ƃ��āA�ƂȂ��Ă��܂��B
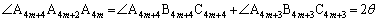 �C
�C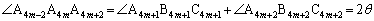
�]����p���������A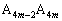 //
// 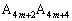 �@����A
�@����A
����Ƈ@���A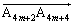 ��x���ɕ��s�ł��B�܂��A
��x���ɕ��s�ł��B�܂��A 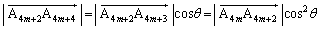
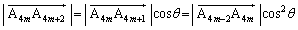 �@����B
�@����B���A
����ƇA���A
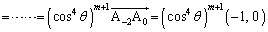 �@����C
�@����C�� 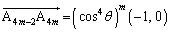 �@(�� �@)������B�ɑ������ƁA
�@(�� �@)������B�ɑ������ƁA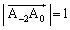 ���A
���A 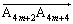 ��x���ɕ��s�Ȃ̂ŁA
��x���ɕ��s�Ȃ̂ŁA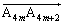 ��x�����琳������
��x�����琳������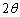 ����������������x�N�g���ł����āA
����������������x�N�g���ł����āA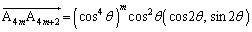 �@(
�@(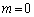 �Ƃ����(1)�̉ł�)�@����D
�Ƃ����(1)�̉ł�)�@����D�C�C�D���A
�Ƃ��āA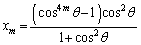 �C
�C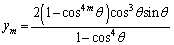 ......[��]
......[��]
(3) (2)�̌��ʂɂ����āA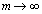 �Ƃ���ƁA
�Ƃ���ƁA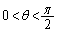 ���A
���A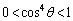 �Ȃ̂ŁA
�Ȃ̂ŁA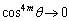 �C
�C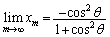 �C
�C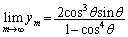 ......[��]�@(���䐔��̋Ɍ����Q��)
......[��]�@(���䐔��̋Ɍ����Q��)
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B