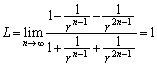等比数列の極限 関連問題
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
この項目については、数列の極限を参照してください。
・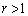 のとき、
のとき、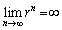
・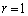 のとき、
のとき、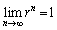
・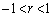 のとき、
のとき、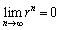
・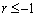 のとき、
のとき、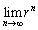 は存在せず、発散する(振動)。
は存在せず、発散する(振動)。
[証明]・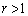 のとき、
のとき、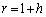 (
(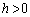 )とおくと、二項定理より、
)とおくと、二項定理より、
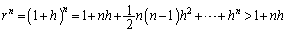
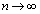 のとき、
のとき、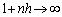 より、
より、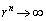
∴ 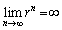
・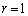 のとき、
のとき、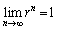 は自明。
は自明。
・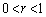 のとき、
のとき、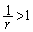 より、
より、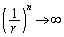
∴ 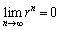
・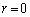 のとき、
のとき、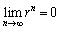 は自明。
は自明。
・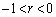 のとき、
のとき、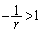 より、
より、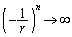
∴ 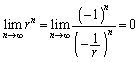
・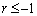 のとき、
のとき、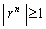 であって、
であって、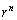 の符号はnが偶数のときに正、nが奇数のときに負、となり、nを大きくしていくときに符号が正負交互に入れ替わるので、数列
の符号はnが偶数のときに正、nが奇数のときに負、となり、nを大きくしていくときに符号が正負交互に入れ替わるので、数列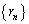 は振動し、
は振動し、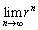 は存在せず、発散する。
は存在せず、発散する。
例1.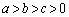 のとき、(1)
のとき、(1) 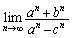 (2)
(2) 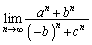
(1) 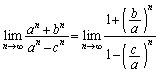 (分母、分子を
(分母、分子を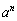 で割る。
で割る。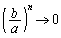 ,
,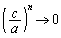 に着目)
に着目)
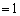
(2) 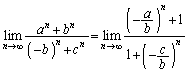 (分母、分子を
(分母、分子を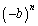 で割る。
で割る。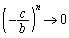 だが、
だが、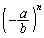 は振動する)
は振動する)
極限は存在しない。
例2.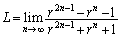
・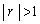 のとき、分母分子を
のとき、分母分子を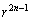 で割ると、
で割ると、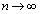 とすると、
とすると、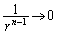 ,
,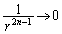 より、
より、
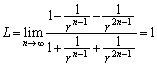
・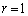 のとき、
のとき、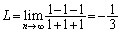
・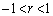 のとき、
のとき、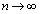 とすると、
とすると、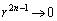 ,
,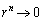 より、
より、
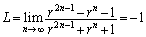
・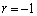 のとき、
のとき、
nが奇数ならば、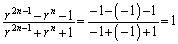
nが偶数ならば、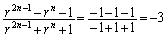
より、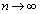 のとき振動するので、Lは存在しない。
のとき振動するので、Lは存在しない。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
数学基礎事項TOP 数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 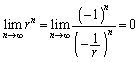
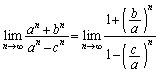 (分母、分子を
(分母、分子を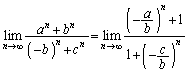 (分母、分子を
(分母、分子を