�啪��㐔�w'08�N[2]
a�Cb��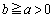 ���݂����萔�Ƃ���Bx�Cy��
���݂����萔�Ƃ���Bx�Cy��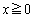 �C
�C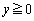 �C
�C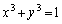 ���݂����Ȃ���ω�����Ƃ��A
���݂����Ȃ���ω�����Ƃ��A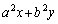 �̂Ƃ蓾��l�͈̔͂����߂�B
�̂Ƃ蓾��l�͈̔͂����߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@2�ϐ������A��������̂��Ƃɂǂ������ω������邩���ׂ���ł��B
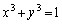 �@����@
�@����@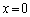 �̂Ƃ�
�̂Ƃ�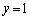
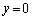 �̂Ƃ�
�̂Ƃ�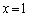
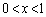 �̂Ƃ�
�̂Ƃ�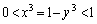 ���
���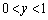 �ł��B
�ł��B
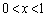 �Ƃ��āA�A���̔����@�ɂ��x�Ŕ��������
�Ƃ��āA�A���̔����@�ɂ��x�Ŕ��������
�� 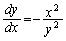
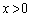 �C
�C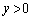 ���A
���A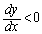
�]���āAx��0����1�܂ő��������y��1����0�܂Ō������܂��B
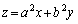 �Ƃ����܂��B
�Ƃ����܂��B
�@�̊W��O��Ƃ��āA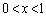 �ɂ����āAz��x�Ŕ�������ƁA
�ɂ����āAz��x�Ŕ�������ƁA
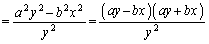 �@����A
�@����A(���̔����́A�@���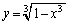 �C�����������
�C�����������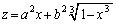 �̔����ɂȂ��Ă��܂�)
�̔����ɂȂ��Ă��܂�) 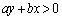 ���A
���A
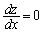 �Ƃ���ƁA
�Ƃ���ƁA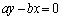
�� 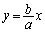 �@����B
�@����B
�@�ɑ������ƁA
�� 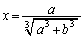
���̂Ƃ��A�B���A
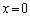 �C
�C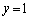 �̂Ƃ��A
�̂Ƃ��A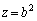
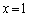 �C
�C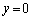 �̂Ƃ��A
�̂Ƃ��A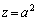
x��0����1�܂ő�������ƁAy��1����0�܂Ō�������̂ŁA�A��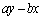 �͌������A
�͌������A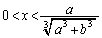 �ɂ����Ă�
�ɂ����Ă�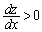 �C
�C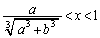 �ɂ����Ă�
�ɂ����Ă�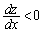 �ł��B
�ł��B
�ȏ���A���̑����\�������܂�(���̑������Q��)�B
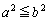 ���A
���A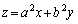 �̂Ƃ肤��͈͂́A
�̂Ƃ肤��͈͂́A
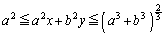 ......[��]
......[��]
�NjL�D�啪���w���A���啪��厞���'94�N[3]�ŁA
a�Cb�Cc�𐳂̒萔�Ƃ���B
(1) 2�̐���x�Cy��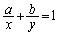 �����Ƃ��A�s����
�����Ƃ��A�s����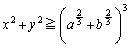 �����藧���Ƃ������B�܂��A��������������x�Cy�̒l�����߂�B
�����藧���Ƃ������B�܂��A��������������x�Cy�̒l�����߂�B (2) O�����_�Ƃ���xyz��Ԃɂ����āA��_P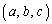 ��ʂ�x���Cy���Cz���̐������ƌ���邷�ׂĂ̕���S���l����B���̂悤�ȕ���S��x���Cy���Cz���ƌ����_���A���ꂼ��AA�CB�CC�Ƃ���B���̂Ƃ��A3�̐���OA�COB�COC��ӂɂ������̂̑Ίp���̒�����S�ƂƂ��ɕω����邪�A���̍ŏ��l�����߂�B
��ʂ�x���Cy���Cz���̐������ƌ���邷�ׂĂ̕���S���l����B���̂悤�ȕ���S��x���Cy���Cz���ƌ����_���A���ꂼ��AA�CB�CC�Ƃ���B���̂Ƃ��A3�̐���OA�COB�COC��ӂɂ������̂̑Ίp���̒�����S�ƂƂ��ɕω����邪�A���̍ŏ��l�����߂�B
�Ƃ�����肪�o�肳��Ă��܂��B�{��Ɠ��n���̖��ł����A������͓��ł��B
(1)�͖{��Ɠ��l�ɉł��܂��B
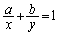 �@����@
�@����@���A���̔����@�Ŕ������A
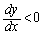 �Ȃ̂ŁAx�����������y�͌������܂��B
�Ȃ̂ŁAx�����������y�͌������܂��B
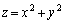 �Ƃ����āAx�Ŕ�������ƁA
�Ƃ����āAx�Ŕ�������ƁA���q��2�߂̃J�b�R�͐��Ȃ̂ŁA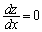 �Ƃ���ƁA
�Ƃ���ƁA 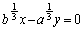
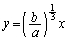 �@����A
�@����A������@�ɑ������ƁA
�� 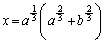 �A���A
�A���A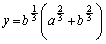
���̂Ƃ��A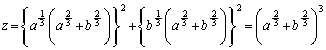 x����������ƁAy�͌�������̂ŁA
x����������ƁAy�͌�������̂ŁA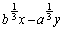 �͑������܂��B
�͑������܂��B
�@�ŁA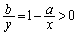 ���A
���A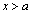 �ł��B
�ł��B
�ȏ���A���̑����\�������܂��B�����\���A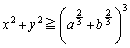
��������������x�Cy�̒l�́A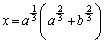 �C
�C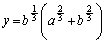
(2)�̕���S�̕����������s���Z�w�K�w���v�͈̂̔͊O�ł����A����S�̕������́AA��x���W�CB��y���W�CC��z���W��p�Cq�Cr�Ƃ��āA
�ƂȂ�܂��B��_P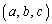 ��ʂ�̂ŁA
��ʂ�̂ŁA �����̂̑Ίp���̒����́A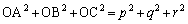 �ł��B(1)��3�����̏ꍇ�Ɋg���������ɂȂ��Ă��܂��Ba�Cb�Cc�Cp�Cq�Cr�����ׂĐ��Ȃ̂ŁA
�ł��B(1)��3�����̏ꍇ�Ɋg���������ɂȂ��Ă��܂��Ba�Cb�Cc�Cp�Cq�Cr�����ׂĐ��Ȃ̂ŁA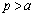 �C
�C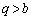 �C
�C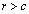 �ł��B
�ł��B
�����Ȃ�3�ϐ��͑�ςȂ̂ŁA1����r���Œ肵�A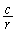 ���E�ӂɈڍ����܂��B
���E�ӂɈڍ����܂��B ���ӂ�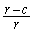 �Ŋ���ƁA
�Ŋ���ƁA 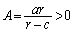 �C
�C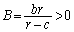 �Ƃ����ƁA(1)���A
�Ƃ����ƁA(1)���A����āA
���̉E�ӂ́A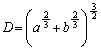 �C
�C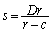 �Ƃ����ƁA
�Ƃ����ƁA �� 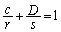 �]���āA�@�Ɠ����`�����Ă��܂��B(1)���A
�]���āA�@�Ɠ����`�����Ă��܂��B(1)���A �� 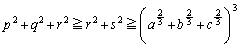 �����ŁA�����̕s�����̓�������������̂́A
�����ŁA�����̕s�����̓�������������̂́A �̂Ƃ��B�E���̕s�����̓�������������̂́A
�̂Ƃ��ŁA���̂Ƃ��A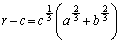 �C
�C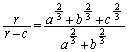 �C
�C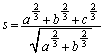
���ǁA�����̕s�����ƉE���̕s�����œ����ɓ�������������̂́A �̂Ƃ��ł��B
�Ίp���̒����̍ŏ��l�́A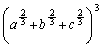 ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 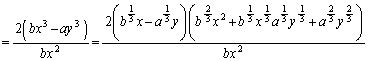
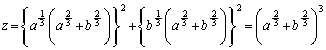
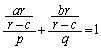
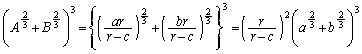
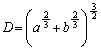 �C
�C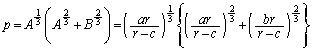
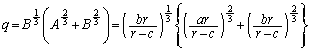
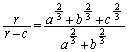 �C
�C