��啶�n���w'08�N[4]
������C�F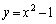 ��
��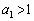 ���݂�������
���݂�������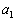 ���l����B���̂Ƃ��A���̖₢�ɓ�����B
���l����B���̂Ƃ��A���̖₢�ɓ�����B
(1) C��̓_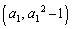 �ɂ�����ڐ���x���Ƃ̌�_��x���W��
�ɂ�����ڐ���x���Ƃ̌�_��x���W��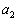 �Ƃ���Ƃ��A
�Ƃ���Ƃ��A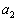 ��
��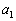 ��p���ĕ\���B
��p���ĕ\���B (2) (1)�ŋ��߂�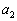 �ɑ��āAC��̓_
�ɑ��āAC��̓_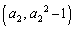 �ɂ�����ڐ���x���Ƃ̌�_��x���W��
�ɂ�����ڐ���x���Ƃ̌�_��x���W��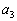 �Ƃ���B���̑�����J��Ԃ��Ăł��鐔���
�Ƃ���B���̑�����J��Ԃ��Ăł��鐔���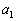 �C
�C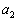 �C����C
�C����C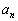 �C����Ƃ���B���̂Ƃ��A���ׂĂ�n�ɑ��āA
�C����Ƃ���B���̂Ƃ��A���ׂĂ�n�ɑ��āA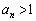 �������B
�������B (3) 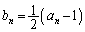 �Ƃ����Ƃ��A���ׂĂ�n�ɑ��āA
�Ƃ����Ƃ��A���ׂĂ�n�ɑ��āA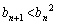 �������B
�������B (4) 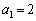 �̂Ƃ��A
�̂Ƃ��A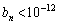 �ƂȂ�n�̒l��1���߂�B�������A�K�v������A
�ƂȂ�n�̒l��1���߂�B�������A�K�v������A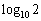 ��
��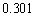 �Ƃ��Čv�Z���Ă悢�B
�Ƃ��Čv�Z���Ă悢�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@��肻�̂��̂́A�Z���^�[�������K�p���x�ł����A�u�j���[�g���@�v�ƌĂ�鐔�l�v�Z�̃A���S���Y�����l�^�ɂ������ł��B(4)�͎����̑����j���[�g���@�̗��_���m���߂悤�A�Ƃ����̂���|�ł��B
(1) C�F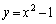
�������āA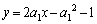
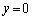 �Ƃ���x���Ƃ̌�_��x���W�́A
�Ƃ���x���Ƃ̌�_��x���W�́A 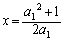 �@(
�@(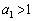 )
)�� 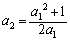 ......[��]
......[��]
(2) C��̓_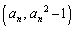 �ɂ�����C�̐ڐ��́A(1)�Ɠ��l�ɂ��āA
�ɂ�����C�̐ڐ��́A(1)�Ɠ��l�ɂ��āA 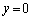 �Ƃ���x���Ƃ̌�_��x���W�́A
�Ƃ���x���Ƃ̌�_��x���W�́A�E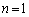 �̂Ƃ��A
�̂Ƃ��A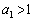 �Ȃ̂Ő��藧���܂��B
�Ȃ̂Ő��藧���܂��B �E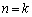 �̂Ƃ����藧�Ɖ��肷��ƁA
�̂Ƃ����藧�Ɖ��肷��ƁA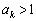 �ł��B
�ł��B �@���A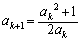
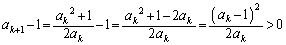 �@(
�@(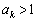 )��
)�� 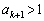 ����āA
����āA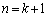 �̂Ƃ��ɂ����藧���܂��B
�̂Ƃ��ɂ����藧���܂��B �ȏ���A���ׂĂ�n�ɑ���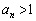 �ƂȂ邱�Ƃ�������܂����B
�ƂȂ邱�Ƃ�������܂����B
(3) 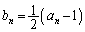 ��n��
��n��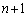 �ɓ���ւ��āA
�ɓ���ւ��āA 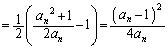 �@(�� �@)
�@(�� �@)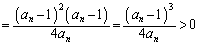 �@(�� (2)���
�@(�� (2)���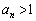 )
)�� 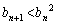
(4) (3)��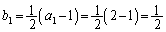 ���A
���A �Ƃ��Ă݂�ƁA
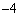 �Ŋ����āA
�Ŋ����āA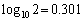 �Ƃ���ƁA
�Ƃ���ƁA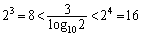 ���A
���A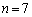 ......[��]
......[��]
�NjL�D�j���[�g���@���l�^�Ƃ�����́A�c�嗝�H'90�N[2]�ȂǁA�ߋ����낢��ȑ�w�ŏo�肳��Ă��܂��B���ł�'97�N���n�O���ŏo�肳��Ă��܂��B
�j���[�g���@�Ƃ����̂́A�����\�Ȋ�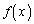 �̌`���^�����āA�������F
�̌`���^�����āA�������F
�̉��𐔒l�I�ɋ��߂���@�ł��B
�K���ȏ����l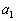 ����o�����āA�Ȑ�
����o�����āA�Ȑ�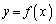 ��̓_
��̓_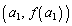 �ɂ�����ڐ��F
�ɂ�����ڐ��F
���l���܂��B���̐ڐ���x���Ƃ̌�_�́A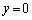 �Ƃ��āA
�Ƃ��āA
�� 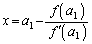 �@(
�@(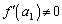 �Ƃ��܂�)
�Ƃ��܂�)
����x��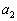 �Ƃ��A�ȉ����l�ɁA
�Ƃ��A�ȉ����l�ɁA
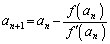 �@���(��)
�@���(��)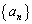 ���߂�ƁA
���߂�ƁA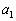 �̎������ǂ�����������A
�̎������ǂ�����������A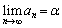 ��
��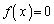 �̉���^���܂��B�Ȃ��Ȃ�A(��)�ɂ����āA
�̉���^���܂��B�Ȃ��Ȃ�A(��)�ɂ����āA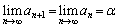 �Ƃ���A
�Ƃ���A
�ƂȂ邩��ł��B
�j���[�g���@�́A�����l�̑I�ѕ��������ƕK�������������܂��A���܂������l��I�т�������}���Ɏ������邱�Ƃ��m���Ă��܂��B�{��ł́A������m���߂邱�Ƃ���|�ɂȂ��Ă��܂��B
�c�����H'90[2]�ł́A
�����グ���Ă��܂����B����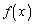 �ł́A
�ł́A
�ƂȂ�܂����A���̐���́A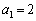 �Ƃ���ƁA
�Ƃ���ƁA
�ƁA�}����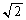 �̐^�̒l�ɋ߂Â��Ă����܂��B
�̐^�̒l�ɋ߂Â��Ă����܂��B
�ł���A
�ƂȂ�A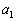 �ɓK���Ȓl��^����A
�ɓK���Ȓl��^����A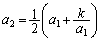 �C
�C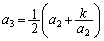 �C����Ƃ��čs���ƁA�}����
�C����Ƃ��čs���ƁA�}����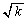 �ɋ߂Â��Ă����܂��B�{��ł́A
�ɋ߂Â��Ă����܂��B�{��ł́A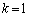 �Ȃ̂ŁA����̑�n��
�Ȃ̂ŁA����̑�n��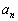 �́An��傫�����Ă�����1�ɋ߂Â��Ă����܂��B
�́An��傫�����Ă�����1�ɋ߂Â��Ă����܂��B
��嗝�n'97�O��[5](I)�ł́A
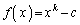 �����グ���Ă��܂����B����
�����グ���Ă��܂����B����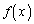 �ł́A
�ł́A
�ƂȂ�܂����A���̑Q������p�����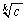 �������܂��B
�������܂��B
�Ƃ���ŁA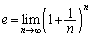 �ł����A
�ł����A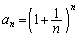 �Œ�߂��鐔��̎����͔��ɒx���A10���ڂł�
�Œ�߂��鐔��̎����͔��ɒx���A10���ڂł�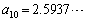 �C100���ڂł�
�C100���ڂł�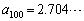 �ƂȂ�Ae�̐^�̒l�A
�ƂȂ�Ae�̐^�̒l�A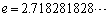 �Ɣ�ׂĂ��Ȃ�J��������܂��B
�Ɣ�ׂĂ��Ȃ�J��������܂��B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B