茶女大理数学'09年[3]
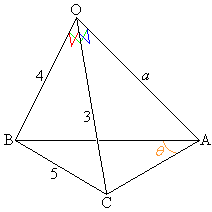
aを正の数とし、次のような条件をみたす四面体OABCを考える。
(1) 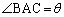 とおく。
とおく。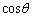 をaを用いて表せ。
をaを用いて表せ。 (2) △ABCの面積をaを用いて表せ。
(3) 球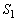 が四面体OABCのすべての面と接しているとする。この球
が四面体OABCのすべての面と接しているとする。この球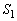 の半径をaを用いて表せ。
の半径をaを用いて表せ。 (4) 四面体OABCのすべての頂点が球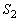 の表面上にあるとする。この球
の表面上にあるとする。この球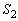 の半径をaを用いて表せ。
の半径をaを用いて表せ。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
解答 難問というわけではないので、素直に空間的に考えて行きたい空間図形の問題です。
(1) 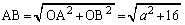
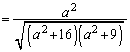 ......[答]
......[答]
(2) θ は三角形の内角で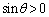 なので、
なので、 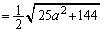 ......[答]
......[答]
(3) 球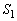 の中心をPとすると、四面体POAB,四面体POBC,四面体POAC,四面体PABCの高さはいずれも球
の中心をPとすると、四面体POAB,四面体POBC,四面体POAC,四面体PABCの高さはいずれも球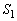 の半径
の半径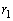 になります。
になります。 三角形OABの面積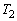 は、
は、 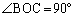 より、三角形OBCの面積
より、三角形OBCの面積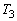 は、
は、三角形OACの面積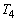 は、
は、 四面体PABC,四面体POAB,四面体POBC,四面体POACの体積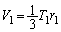 ,
,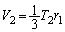 ,
,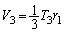 ,
,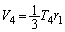 の和は、四面体OABCの体積Vになります。
の和は、四面体OABCの体積Vになります。 ∴ 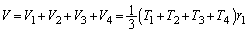
∴ 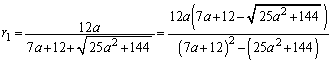
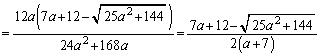 ......[答]
......[答]
(4) 球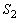 の中心Qは、4頂点O,A,B,Cから等距離の点です。
の中心Qは、4頂点O,A,B,Cから等距離の点です。 OA,OB,OCが互いに垂直であることと、Qが、OA,OB,OCの各中点を通り、それぞれ、OA,OB,OCに垂直な3平面の交点になることから、OQは、Oにつながる3辺の長さが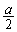 ,2,
,2,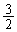 である直方体の対角線であって、求める半径OQは、
である直方体の対角線であって、求める半径OQは、 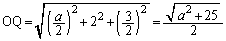 ......[答]
......[答]
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 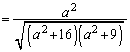 ......[答]
......[答]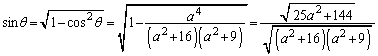
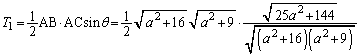
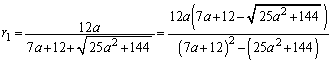
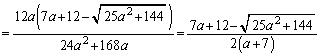 ......[答]
......[答]