茶女大文教数学'09年[1]
正の整数nに対しnの正の約数すべての和を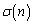 とおく。ただし、1とnもnの約数とする。以下の問いに答えよ。
とおく。ただし、1とnもnの約数とする。以下の問いに答えよ。
(1) 素数p,正の整数aに対し、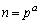 とおく。
とおく。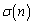 をpとaで表せ。
をpとaで表せ。 (2) 相異なる素数p,q,正の整数a,b,に対し、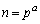 ,
,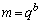 とおく。このとき、
とおく。このとき、 が成立することを証明せよ。
(3) 正の整数aについて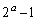 が素数とする。このとき、
が素数とする。このとき、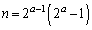 とおくと、
とおくと、 が成立することを証明せよ。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
解答 約数に関するよく知られた事実を示す問題です。なお、整数を参照してください。
です。その和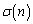 は、
は、
(2) 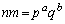 の約数は、
の約数は、 1,p,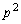 ,・・・,
,・・・,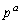 ,q,
,q,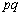 ,
,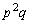 ,・・・,
,・・・,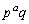 ,
,
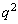 ,
,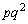 ,
,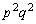 ,・・・,
,・・・,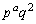 ,
, ・・・・・・
です。その和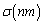 は、
は、 (証明終)
(3) 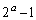 は奇数の素数なので、(2)で、
は奇数の素数なので、(2)で、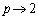 ,
,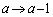 ,
,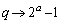 ,
,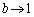 とすることにより、
とすることにより、 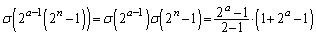 (∵ (1),また、
(∵ (1),また、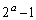 は素数)
は素数)(証明終)
追記.(1)について、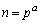 の約数の個数
の約数の個数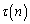 は、
は、
で与えられることがわかります。
(2)については、自然数nが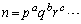 と素因数分解されるとき、nの約数の個数
と素因数分解されるとき、nの約数の個数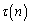 ,約数の総和
,約数の総和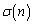 について、
について、
と一般化できます。
上記を含め、(3)に関する背景については、高木貞治著「初等整数論講義」(共立出版)のp.13〜p.15を参照してください。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。