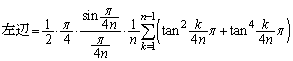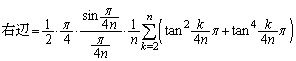����������吔�w'09�N[4]
n��2�ȏ�̎��R���Ƃ��Ak��n�ȉ��̎��R���Ƃ���B���W���ʏ�̌��_O�̂܂���x����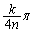 ��]����������
��]����������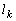 �Ƃ��A
�Ƃ��A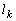 �ƕ�����
�ƕ�����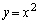 �Ƃ�2�̌�_�̂������_�ȊO�̓_��
�Ƃ�2�̌�_�̂������_�ȊO�̓_��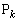 �Ƃ���B�܂��A
�Ƃ���B�܂��A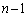 �ȉ��̎��R��k�ɂ��āA�O�p�`
�ȉ��̎��R��k�ɂ��āA�O�p�`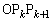 �̖ʐς�
�̖ʐς�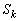 �Ƃ����B�ȉ��̖₢�ɓ�����B
�Ƃ����B�ȉ��̖₢�ɓ�����B
(1) �s��ϕ�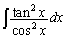 �����߂�B
�����߂�B (2) ���ׂĂ�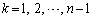 �ɂ��āA���̕s���������藧���Ƃ������B
�ɂ��āA���̕s���������藧���Ƃ������B (3) �Ɍ��l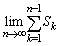 �����߂�B
�����߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@�͂��݂�������Ƃ��ɁA�͂��ނ��̂��敪���ϖ@�ɂȂ�A�Ƃ����A�Ɍ��̊�{���ł��B
(1) 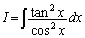
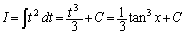 (C�F�ϕ��萔) ......[��]
(C�F�ϕ��萔) ......[��]
(2) ����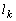 ��x���̂Ȃ��p��
��x���̂Ȃ��p��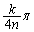 �ŁA���̌X����
�ŁA���̌X����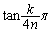
�@�C�A��A������ƁA
�@�C�A��2��_�̂������_�ȊO�̓_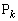 ��x���W�́A
��x���W�́A 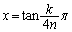 (
(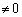 )
)�A���A�_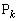 �̍��W��
�̍��W��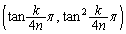 �C
�C 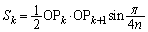 (
(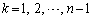 )
)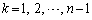 �̂Ƃ��A
�̂Ƃ��A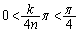 �C
�C (
(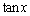 ��
��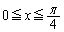 �ɂ����đ�����)����āA
�ɂ����đ�����)����āA�� 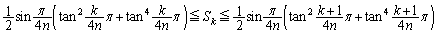
(3) (2)�̕s������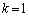 ����
����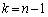 �܂ŕӁX�������킹�邱�Ƃɂ��A
�܂ŕӁX�������킹�邱�Ƃɂ��A 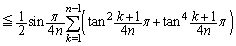 �@����B
�@����B������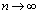 �Ƃ���ƁA
�Ƃ���ƁA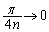 ���A
���A 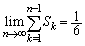 ......[��]
......[��]
�NjL�D��L���敪���ϖ@�ŁA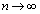 �̂Ƃ��A
�̂Ƃ��A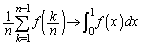 �C
�C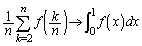 �Ƃ��Ă���̂�s�v�c�Ɏv���������������邩���m��܂���B
�Ƃ��Ă���̂�s�v�c�Ɏv���������������邩���m��܂���B
���ȏ��ł́A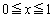 �ŘA���Ȋ�
�ŘA���Ȋ�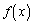 ��n�̘a�̋Ɍ��ɂ��āA
��n�̘a�̋Ɍ��ɂ��āA
�Ƃ��Ă��܂��B
�ł����A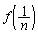 �C
�C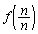 �͗L���Ȓl�Ȃ̂ŁA
�͗L���Ȓl�Ȃ̂ŁA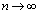 �̂Ƃ��A
�̂Ƃ��A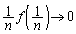 �C
�C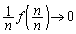 �ł��B
�ł��B
�ł���A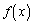 ��
��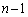 �̘a�̋Ɍ��ɂ��āA
�̘a�̋Ɍ��ɂ��āA
�ł��B�����Ƌɒ[�Ȃ��Ƃ������A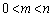 �����L���Ȑ���m���Ƃ�Ƃ��A
�����L���Ȑ���m���Ƃ�Ƃ��A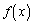 ��
��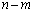 �̘a�̋Ɍ��ɂ��āA
�̘a�̋Ɍ��ɂ��āA
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B