���s�{���吔�w'09�N[1]
�萔a�������Ƃ��A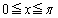 �Ƃ���B��
�Ƃ���B��
�Ƃ���B�ȉ��̖₢�ɓ�����B
(1)  �Ƃ���Ƃ��At�̒l�͈̔͂����߂�B
�Ƃ���Ƃ��At�̒l�͈̔͂����߂�B (2) y��t�̎��ŕ\���B
(3)  ���˂ɐ��藧�悤�ɁAa�̒l�͈̔͂����߂�B
���˂ɐ��藧�悤�ɁAa�̒l�͈̔͂����߂�B (4) ������ ��3�ȏ�̈قȂ�����������悤�ɁAa�̒l�͈̔͂����߂�B
��3�ȏ�̈قȂ�����������悤�ɁAa�̒l�͈̔͂����߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@�O�p����2���������E2�����̗Z�����ł��B
�����ŁAα�́A �C
�C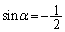 �����p�ŁA
�����p�ŁA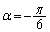
�� 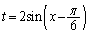
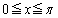 ���
���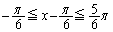 �C
�C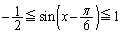
��  ......[��]
......[��]
(2) 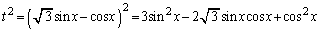
�����y�̎�������ׂ�ƁA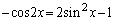 ���A
���A ������A
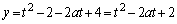 ......[��]
......[��]
(3) 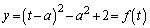
�Ƃ����܂��B���̈ʒu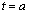 ���A(1)�ŋ��߂�
���A(1)�ŋ��߂� �Ƃ����͈͂̂ǂ��ɂ��邩�A(i) �͈͂��獶��(
�Ƃ����͈͂̂ǂ��ɂ��邩�A(i) �͈͂��獶��(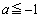 )�@(ii) �͈͓��̍���(
)�@(ii) �͈͓��̍���(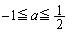 )�@(iii) �͈͓��̉E��(
)�@(iii) �͈͓��̉E��(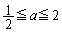 )�@(iv) �͈͂���E��(
)�@(iv) �͈͂���E��( ) �Ƃ������Ƃŕ��ނ��āA
) �Ƃ������Ƃŕ��ނ��āA �̍ő�ŏ����l���܂�(2�����̍ő�ŏ����Q��)�B
�̍ő�ŏ����l���܂�(2�����̍ő�ŏ����Q��)�B (i)  �̂Ƃ��A
�̂Ƃ��A �ɂ�����y�͒P�������Ȃ̂ŁA
�ɂ�����y�͒P�������Ȃ̂ŁA �ŏ��l�F
�ő�l�F
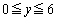 �ƂȂ邽�߂ɁA
�ƂȂ邽�߂ɁA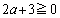 ����
���� 
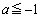 ���A�������a�͂���܂���B
���A�������a�͂���܂���B (ii)  �̂Ƃ��A��
�̂Ƃ��A��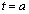 �͔͈͂̍����ɂ����āA
�͔͈͂̍����ɂ����āA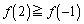 �ł��B
�ł��B �ŏ��l�F
�ő�l�F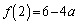
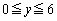 �ƂȂ邽�߂ɁA
�ƂȂ邽�߂ɁA ����
���� 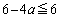
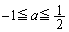 �ƍ��킹�āA
�ƍ��킹�āA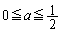 �@����@
�@����@ (iii)  �̂Ƃ��A��
�̂Ƃ��A�� �͔͈͂̉E���ɂ����āA
�͔͈͂̉E���ɂ����āA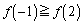 �ł��B
�ł��B �ŏ��l�F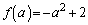
�ő�l�F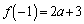
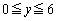 �ƂȂ邽�߂ɁA
�ƂȂ邽�߂ɁA ����
���� 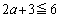
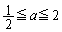 �ƍ��킹�āA
�ƍ��킹�āA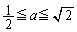 �@����A
�@����A (iv) 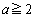 �̂Ƃ��A
�̂Ƃ��A �ɂ�����y�͒P�������Ȃ̂ŁA
�ɂ�����y�͒P�������Ȃ̂ŁA �ŏ��l�F
�ő�l�F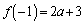
 �ƂȂ邽�߂ɁA
�ƂȂ邽�߂ɁA ����
���� 
 ���A�������a�͂���܂���B
���A�������a�͂���܂���B �@�C�A���A ......[��]
......[��]
(4) 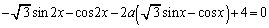 �C
�C �@����B
�@����B �̉��́A
��A�������Ƃ��̉��ł��B�C�̎������̌��͑����Ă�2�ł��B�D��t�̒l���Œ肷��Ƃ��A�������̌��͑����Ă�2�ł��B
�]���āA�B��3�ȏ�̑��قȂ�����������Ƃ��A(1)���C�� �͈̔͂�2�̑��قȂ�������������܂��B�@����E
�͈̔͂�2�̑��قȂ�������������܂��B�@����E
���̂Ƃ��A�C�̉�t�ɑ��ćD�͎����I��1�܂���2�̎������������A��ӂ����܂��B
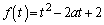 �Ƃ��āA�E���(2���������̉��̔z�u���Q��)�A
�Ƃ��āA�E���(2���������̉��̔z�u���Q��)�A �C�̔��ʎ��F �@����F
�@����F
 �̎��F
�̎��F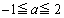 �@����G
�@����G
�[�F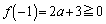 �C
�C �@����H
�@����H �F���A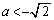 �C
�C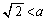 �@����I
�@����I
�H���A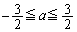 �@����J
�@����J
�I���G���J���A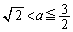 ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B